Based on appendix A in
The Way of Z.
Links to more Z examples.
This page looks best when this 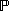 and this X are
about the same size:
and this X are
about the same size:  X. See these viewing tips.
X. See these viewing tips.
Names
Definitions
Logic
Sets and expressions
Relations
Functions
Numbers
Sequences
Axiomatic definition
Schema
Generic Definition
Schema Calculus
Conventions
Other Z pages
Acknowledgements
| a,b | identifiers |
| d,e | declarations (e.g., a: A; b, ...: B ...) |
| f,g | functions |
| m,n | numbers |
| p,q | predicates |
| s,t | sequences |
| x,y | expressions |
| A,B | sets |
| C,D | bags |
| Q,R | relations |
| S,T | schemas |
| X | schema text (e.g., d, d | p, or S) |
| a == x | Abbreviation definition |
| a ::= b | ... | Free type definition |
| [a] | Introduction of a given set (or [a,...]) |
| a _ | Prefix operator |
| _ a | Postfix operator |
| _ a _ | Infix operator |
| true | Logical true constant |
| false | Logical false constant |
 p p | Logical negation, not |
p  q q | Logical conjunction, and |
p  q q | Logical disjunction, or |
p  q q | Logical implication |
p  q q | Logical equivalence |
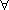 X X  q q | Universal quantification |
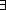 X X  q q | Existential quantification |
(let a == x; ...  p) p) | Local definition |
| x = y | Equality |
x  y y | Inequality |
x  A A | Set membership |
x  A A | Non-membership |
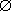 | Empty set |
A 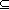 B B | Set inclusion |
A  B B | Strict set inclusion |
| { x, y, ... } | Set display |
{ X  x } x } | Set comprehension |
(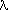 X X  x) x) | Lambda expression |
(let a == x; ...  y) y) | Local definition |
| if p then x else y | Conditional expression |
| (x,y, ...) | Tuple |
| (x,y) | Pair |
A  B B  ... ... | Cartesian product |
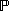 A A | Power set |
A  B B | Set intersection |
A 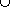 B B | Set union |
| A \ B | Set difference |
| first x | First element of an ordered pair |
| second x | Second element of an ordered pair |
| # A | Number of elements in a set |
A 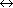 B B | Binary relation (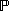 (A (A  B)) B)) |
a 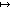 b b | Maplet ((a,b)) |
| dom R | Domain of a relation |
| ran R | Range of a relation |
Q 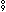 R R | Forward relational composition |
Q  R R | Backward relational composition (R 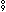 Q) Q) |
A 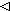 R R | Domain restriction |
A 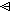 R R | Domain anti-restriction |
A 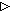 R R | Range restriction |
A 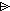 R R | Range anti-restriction |
R 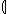 A A 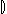 | Relational image |
| R ~ | Inverse of relation |
| R + | Transitive closure |
Q  R R | Relational overriding |
| a R b | Infix relation |
A 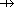 B B | Partial functions |
A 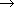 B B | Total functions |
A 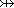 B B | Partial injections |
A 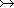 B B | Total injections |
A 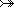 B B | Bijections |
| f x | Function application (or f(x)) |
 | Set of integers |
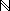 | Set of natural numbers { 0, 1, 2, ... } |
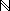 1 1 | Set of strictly positive numbers { 1, 2, ... } |
| m+n | Addition |
| m-n | Subtraction |
| m*n | Multiplication |
| m div n | Division |
| m mod n | Remainder (modulus) |
m  n n | Less than or equal |
| m < n | Less than |
m  n n | Greater than or equal |
| m > n | Greater than |
| m .. n | Number range |
| min A | Minimum of a set of numbers |
| max A | Maximum of a set of numbers |
| seq A | Set of finite sequences |
| seq1 A | Set of non-empty finite sequences |
| iseq A | Set of finite injective sequences |
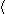 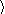 | Empty sequence |
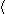 x, y, ... x, y, ... 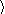 | Sequence display |
s 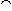 t t | Sequence concatenation |
| head s | First element of a sequence |
| tail s | All but the head element of a sequence |
| last s | Last element of a sequence |
| front s | All but the last element of a sequence |
| s in t | Sequence segment relation |
S  [ X ] [ X ] | Horizontal schema |
| [ T; ... | ... ] | Schema inclusion |
| z.a | Component selection (given z:S) |
 S S | Binding |
 S S | Schema negation |
S  T T | Schema conjunction |
S  T T | Schema disjunction |
S 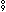 T T | Schema composition |
| S >> T | Schema piping |
| a? | Input to an operation |
| a! | Output from an operation |
| a | State component before an operation |
| a' | State component after an operation |
| S | State schema before an operation |
| S' | State schema after an operation |
 S S | Change of state |
 S S | No change of state |
Z mathematical tool-kit
defines the operators shown in this glossary.
Z examples in web pages.
Z2HTML tool for translating
LaTeX documents with Z markup to HTML web pages.
Z home page
with FAQ and links to publications, tools, and meetings.
Back to top
This page is based on the more complete
PostScript glossary
by
Jonathan Bowen
at the
Z home page.
Jonathan Jacky /
Department of Radiation Oncology
Box 356043
University of Washington /
Seattle, Washington 98195-6043 / USA
Tel (206) 598-4117 / Fax (206) 598-6218
E-mail: jon@u.washington.edu
![]() and this X are
about the same size:
and this X are
about the same size: ![]() X. See these viewing tips.
X. See these viewing tips.
p
q
q
q
q
X
q
X
q
p)
y
A
A
B
B
x }
X
x)
y)
B
...
A
B
B
B
(A
B))
b
R
R
Q)
R
R
R
R
A
R
B
B
B
B
B
1
n
n
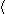
x, y, ...
t
[ X ]
S
S
T
T
T
S
S