Dynamic Disorder in Supported Metal Nanocatalysts
Nanoparticle materials are ubiquitous in heterogeneous catalytic processes and there is broad interest in their physical and chemical properties at the atomic level. Global experimental probes such as EXAFS, XANES and XPS, however, reveal only their ensemble characteristics, obscuring details of their internal structure. My research [F. D. Vila et al., Phys. Rev. B 78, 121404(R) (2008)] focuses on the nanoscale theoretical modelling of the structure and x-ray response of these systems. It provides a deep understanding of the intra-particle heterogeneity of these systems, and their changes under realistic conditions. [F. D. Vila et al., J. Phys. Chem. C 117, 12446 (2013)] My DFT/MD simulations reveal (see video on right) that both structure and charge are inhomogeneous, and fluctuate dynamically over several time-scales. These range from fast (200-400 fs) bond vibrations to slow fluxional bond breaking (>10 ps). More interestingly, the equilibrium points of the vibrations are not static, but rather driven by the stochastic motion of the center of mass over 1-4 ps time-scales. This results in “dynamic structural disorder” (DSD), semi-melted cluster surfaces, atomic-segregation, and modulation of adsorbate dynamics. [J. J. Rehr and F. D. Vila, J. Chem. Phys. 140, 134701 (2014)] These fluctuations also affect the catalytic properties of the nanoparticles by changing the reaction landscape (Figure 1).
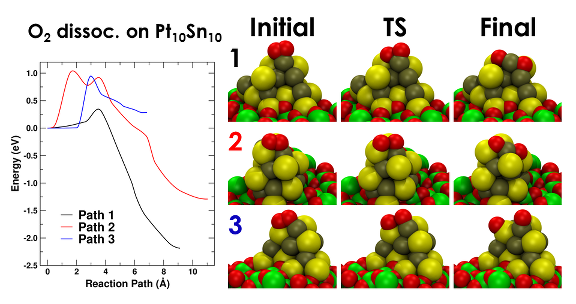
Figure 1: Reaction paths for the dissociation of O2 on Pt10Sn10 as a function of nanoparticle disorder. These reaction paths show different behaviors, from exothermic to endothermic thermodynamics. The role of disorder is clear in path 1, where the incipient formation of a Sn-O bond stabilizes the transition state.
Ab Initio Debye-Waller Factors
Thermal and structural disorder effects are of crucial importance in X-ray spectroscopy since they lead to strong exponential damping of the fine structure. This damping is dominated by the XAFS Debye-Waller factor \( W = \mathrm{exp}\left(-2\sigma^{2}_{R} k^2 \right)\) where \( \sigma^{2}_{R} \) is the mean square relative displacement (MSRD) for path \(R\). The MSRD is defined by the thermal average $$ \sigma^{2}_{R} = \left< \left( R - \bar{R} \right)^2 \right>, $$ where \( R \) and \( \bar{R} \) are the instantaneous and mean path lengths, respectively. In the quasi-harmonic approximation, the average can be computed as a sum over vibrational or phonon eigenmodes or, alternatively, in terms of the projected vibrational density of states \( \rho_R \left( \omega \right) \) or VDOS, and the Debye integral: $$ \sigma^{2}_{R} = \frac{\hbar}{2\mu_R} \int_{0}^{\infty} \frac{1}{\omega} \mathrm{coth} \left( \frac{\beta \hbar \omega}{2} \right) \rho_R \left( \omega \right) d\omega, $$ where \( \mu_R \) is the reduced mass for path \( R \). Following on work by Poiarkova and Rehr, I have implemented [F. D. Vila et al., Phys. Rev. B 76, 014301 (2007)] an efficient, ab initio way to compute the PDOS from the imaginary part of lattice dynamical Green's function $$ \rho_R \left( \omega \right) = -\frac{2\omega}{\pi} \mathrm{Im} \left< 0 \left| \frac{1}{\omega^2 - \mathbf{D} + i\epsilon} \right| 0 \right> \simeq \sum_{\nu=1}^{N} w_{\nu} ~ \delta \left(\omega - \omega_{\nu} \right). $$ Here \( \left| 0 \right> \) is a vector representing a normalized mass-weighted displacement of the atoms along the multiple-scattering path \( R \). The lattice dynamical Green's function is represented in the form of a continued fraction obtained from the iterative Lanczos algorithm. This yields a \(N\)-pole representation for the VDOS where \( \omega_{\nu} \) and \( w_{\nu} \) are, respectively, the pole frequencies and weights of pole \( \nu \). The dynamical matrix of force constants or Hessian, \(\mathbf{D} \), is the main ingredient required for the calculation of theoretical MSRDs and is defined as $$ D_{jl\alpha,j'l'\beta} = \left( M_j M_{j'} \right)^{-1/2} \frac{\partial^2 E}{\partial u_{jl\alpha} \partial u_{j'l'\beta}}, $$ where \( u_{jl\alpha} \) and \( M_j \) are the \( \alpha = \left\{x,y,z\right\} \) Cartesian displacement and mass of atom \(j\) in unit cell \(l\), respectively, and \(E\) is the internal energy of the system. I have implemented this method in the DMDW module of FEFF. For molecular systems, \( \mathbf{D} \) can be computed and imported from quantum chemistry packages like Gaussian, NWChem, Orca, etc. For solids, the dynamical matrix can be obtained using ABINIT, VASP and Quantum ESPRESSO. Besides the MSRD, the DMDW module can be used to compute thermal expansion coefficients and vibrational free energies.
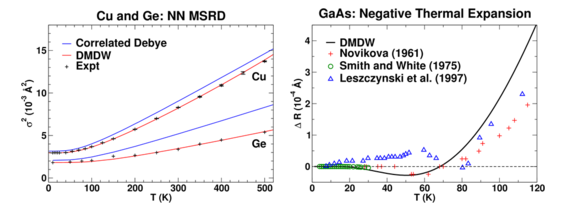
Figure 2: Left: Comparison of the DMDW, Correlated Debye, and experimental near-neighbor MSRD for Cu and Ge. Right: Comparison of the DMDW and experimental thermal expansion for GaAs.
Real-Time Electron Dynamics
In the past decade, Time-Dpendent Density Funcitonal Theory (TDDFT) has become a versatile method for computing electronic response. Real time (RT) variants of this method are particularly useful in the linear and non-linear regimes when arbitrary electromagnetic perturbations such as pulses are used. I am part of the development of RT-Siesta,[Y. Takimoto et al., J. Chem. Phys. 127, 154114 (2007)] an efficient implementation of RT-TDDFT based on the Siesta LCAO approach. RT-Siesta solves the time-dependent Kohn-Sham equation by time-evolving the Kohn-Sham states in the presence of an external electric field:
$$ i \frac{\partial\Psi}{\partial t} = H\left(t\right) \Psi \qquad \longrightarrow \qquad \Psi\left(t\right) = T \mathrm{exp}\left( -i \int_{0}^{t} H\left(t'\right) dt' \right) \Psi\left(0\right) \\ H = -\frac{1}{2}\nabla^2 + V_{ext}\left(\mathbf{r},t\right) + V_H\left[\rho\right]\left(\mathbf{r},t\right) + V_{xc}\left[\rho\right]\left(\mathbf{r},t\right) $$
The optical properties are determined from the total dipole moment:
$$ \mathbf{p}\left(t\right) = \int \rho\left(\mathbf{r},t\right)\mathbf{r} d^3\mathbf{r} \\ \underbrace{\chi_{ij}^{(1)}\left(\omega\right)=\delta p_i\left(\omega\right)/E_j\left(\omega\right)=\alpha_{ij}\left(\omega\right)}_\text{Linear Response} \qquad \underbrace{\sigma\left(\omega\right) \sim \omega ~ \mathrm{Im} \left<\alpha\left(\omega\right)\right>}_\text{Absorption} $$
In RT-Siesta the states are represented in an LCAO basis, thus we just propagate the coefficients \(c\):
$$ i \frac{\partial c\left(t\right)}{\partial t} = S^{-1}H\left(t\right) c\left(t\right) $$
where \(S\) is the basis set overlap matrix. The evolution is done with a Crank-Nicolson propagator:
$$ c\left(t+\Delta t\right) = \frac{1-iS^{-1}H\left(t+\Delta t/2\right)\Delta t/2}{1+iS^{-1}H\left(t+\Delta t/2\right)\Delta t/2}c\left(t\right) + \mathcal{O} \left(\Delta t^2 \right) $$
I have implemented a predictor-corrector scheme for the propagator that ensures time-reversibility, thus enabling very long time steps. The method has been applied to the simulation of full optical spectra in complex chromophores, and the computation of their NLO response over a range of frequencies (Figure 3). Recent developments have extended RT-SIESTA to compute core spectroscopies such as XAS, XES, and response to core perturbations.
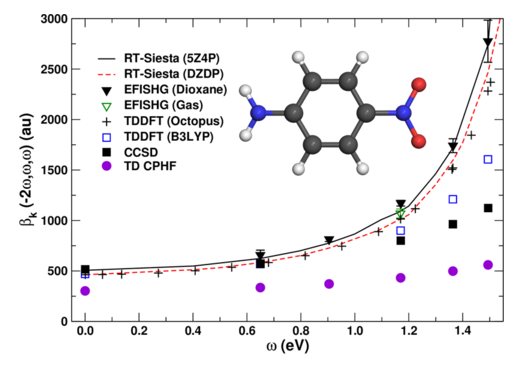
Figure 3: NLO optical response of para-nitroaniline.