Based on appendix D in
The Way of Z.
Links to more Z examples.
This page looks best when this  and this X are
about the same size:
and this X are
about the same size:  X. See these viewing tips.
X. See these viewing tips.
The Z mathematical tool-kit is a collection of types and operators
somewhat like a standard library of types and functions in a
programming language.
The definitions in the tool-kit build up all the Z operators from
a few fundamental constructs in logic and set theory.
The tool-kit uses generic definitions very heavily: X, Y, and Z
stand for any type, S and T are sets of any type, and Q and R
are binary relations between any two types. The toolkit also makes
extensive use of patterns in abbreviation definitions, for example it
defines the binary relation symbol  by X
by X  Y ==
Y ==  (X
(X  Y).
Y).
In a few places I've used English paraphrases for predicates, where
the formal definition uses constructs or concepts not defined here.
These selections from the tool-kit are based on the
Reference Manual,
which defines additional types and operators.
Sets
Pairs and binary relations I
Pairs and binary relations II
Pairs and binary relations III
Numbers and arithmetic
Functions
Sequences
Other Z pages
Glossary
 | - | Empty set: a set that has no elements |
x  S S | - | Non-membership: x is not an element of S |
S 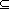 T T | - | Subset: all elements of S belong to T |
S  T T | - | Proper subset: S is a subset of T and S is not equal to T |
S  T T | - | Union: the set of elements in either S or T |
S  T T | - | Intersection: the set of elements in both S and T |
| S \ T | - | Set difference: the set of elements in S that are not in T |
Definitions
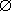 [X] == { x: X | false } [X] == { x: X | false } |
 |
| [X] |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
| _  _ : X _ : X   X X |
| _ 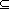 _, _ _, _  _ : _ :  X X   X X |
| _ 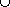 _ , _ _ , _  _, _ \ _: _, _ \ _:  X X   X X   X X |
 |
 |
 |
 |
 |
| 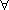 x: X; S, T: x: X; S, T:  X X  |
|  |
|  x x  S S   (x (x  X) X)  |
|  |
|  (S (S 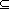 T T  ( (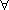 x: X x: X  x x  S S  x x  T)) T))  |
|  |
|  (S (S  T T  S S 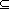 T T  S S  T) T)  |
|  |
|  S S 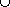 T = { x: X | x T = { x: X | x  S S  X X  T } T }  |
|  |
|  S S  T = { x: X | x T = { x: X | x  S S  X X  T } T }  |
|  |
|  S \ T = { x: X | x S \ T = { x: X | x  S S  X X  T } T } |
|  |
 |
 |
Glossary
| (x,y) | - | The pair x,y |
x 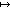 y y | - | Maplet: x maps to y, same as (x,y) |
| first p | - | First element of pair p |
| second p | - | Second element of pair p |
| id X | - | Identity relation |
X  Y Y | - | Binary relation |
| dom R | - | Domain: the set of first elements of all pairs in R |
| ran R | - | Range: the set of second elements of all pairs in R |
Definitions
X  Y == Y ==  (X (X  Y) Y) |
 |
id X == { x: X  x x 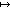 x } x } |
 |
| [X,Y] |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
| first: X  Y Y  X X |
| second: X  Y Y  Y Y |
| _ 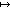 _ : X _ : X  Y Y  X X  Y Y |
| dom: (X  Y) Y)   X X |
| ran: (X  Y) Y)   Y Y |
 |
 |
 |
 |
 |
| 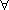 x: X; y: Y; R: X x: X; y: Y; R: X  Y Y  |
|  |
|  first(x,y) = x first(x,y) = x  |
|  |
|  second(x,y) = y second(x,y) = y  |
|  |
|  x x 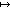 y = (x,y) y = (x,y)  |
|  |
|  dom R = { x: X; y: Y | x R y dom R = { x: X; y: Y | x R y  x } x }  |
|  |
|  ran R = { x: X; y: Y | x R y ran R = { x: X; y: Y | x R y  y } y } |
|  |
 |
 |
Glossary
S 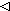 R R | - | Domain restriction: the pairs in R whose first element is in S |
R 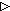 T T | - | Range restriction: the pairs in R whose second element is in T |
S 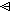 R R | - | Domain antirestriction: the pairs in R whose first element is not in S |
R 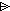 T T | - | Range antirestriction: the pairs in R whose second element is not in T |
| R ~ | - | Relational inverse: the pairs in R, |
| | but with first and second elements exchanged |
R 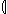 S S 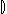 | - | Relational image: the second elements of pairs |
| | in R whose first element is in S. |
R  Q Q | - | Overriding: all pairs in R or Q, |
| | except pairs in R whose first element is also in Q. |
| R + | - | Transitive closure of R |
Definitions
 |
| [X,Y] |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
| _ 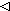 _, _ _, _ 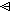 _ : _ :  X X  (X (X  Y) Y)  X X  Y Y |
| _ 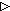 _, _ _, _ 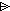 _ : (X _ : (X  Y) Y)   Y Y  X X  Y Y |
| _ ~ : (X  Y) Y)  (Y (Y  X) X) |
| _ 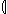 _ _ 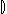 : (X : (X  Y) Y)   X X   Y Y |
| _  _ : (X _ : (X  Y) Y)  (X (X  Y) Y)  (X (X  Y) Y) |
| _ + : (X  X) X)  (X (X  X) X) |
 |
 |
 |
 |
 |
| 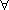 x: X; y: Y; S: x: X; y: Y; S:  X; T: X; T:  Y; Q, R: X Y; Q, R: X  Y Y  |
|  |
|  S S 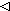 R = { x: X; y: Y | x R = { x: X; y: Y | x  S S  x R y x R y  x x 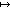 y } y }  |
|  |
|  S S 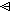 R = { x: X; y: Y | x R = { x: X; y: Y | x  S S  x R y x R y  x x 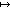 y } y }  |
|  |
|  R R 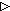 T = { x: X; y: Y | x R y T = { x: X; y: Y | x R y  y y  T T  x x 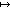 y } y }  |
|  |
|  R R 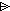 T = { x: X; y: Y | x R y T = { x: X; y: Y | x R y  y y  T T  x x 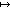 y } y }  |
|  |
|  R ~ = { x: X; y: Y | x R y R ~ = { x: X; y: Y | x R y  y y 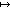 x } x }  |
|  |
|  R R 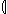 S S 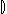 = { x: X; y: Y | x = { x: X; y: Y | x  S S  x R y x R y  y } y }  |
|  |
|  Q Q  R = ((dom R) R = ((dom R) 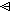 Q) Q) 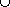 R R |
|  |
|  ... predicate for _ + omitted ... ... predicate for _ + omitted ... |
|  |
 |
 |
Glossary
Q 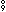 R R | - | Relational composition: Q composed with R |
R  Q Q | - | Backward relational composition, same as Q 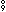 R R |
Definitions
 |
| [X,Y,Z] |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
| _ 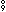 _ : (X _ : (X  Y) Y)  (Y (Y  Z) Z)  (X (X  Z) Z) |
| _  _ : (Y _ : (Y  Z) Z)  (X (X  Y) Y)  (X (X  Z) Z) |
 |
 |
 |
 |
 |
| 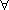 Q: X Q: X  Y; R: Y Y; R: Y  Z Z  |
|  Q Q 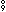 R = R R = R  Q = { x: X; y: Y; z: Z | x Q y Q = { x: X; y: Y; z: Z | x Q y  y R z y R z  x x 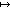 z } z } |
 |
 |
Glossary
 | - | The set of integers |
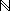 | - | The set of natural numbers, starting with zero |
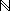 1 1 | - | The set of strictly positive numbers, starting with one |
| +,-,* | - | Arithmetic operators: addition, subtraction, multiplication |
| div,mod | - | Arithmetic operators: integer division and remainder (modulus) |
<, | - | Comparison: less than, less than or equal |
>,  | - | Comparison: greater than, greater than or equal |
| i .. j | - | Number range: the set of numbers starting with i up through j |
| min S | - | Mininum: the smallest element in S, if any |
| max S | - | Maximum: the largest element in S, if any |
| # S | - | Size: the number of elements in S |
 1 1 | - | Non-empty sets |
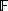 | - | Finite sets |
Definitions
[ ] ] |
 |
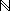 == { n: == { n:  | n | n  0 } 0 } |
 |
 1 == 1 ==  \ { 0 } \ { 0 } |
 |
 1 X == { S: 1 X == { S:  X | S X | S  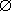 } } |
 |
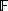 X == { S: X == { S:  X | ... S is finite ... } X | ... S is finite ... } |

|
| _ + _, _ - _, _* _ :      |
| _ div _, _ mod _ :   ( ( \ { 0 }) \ { 0 })   |
| _ - :    |
| _ < _, _  _, _ _, _  _, _ > _ : _, _ > _ :    |
| _ .. _ :       |
| #: 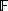 X X  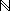 |
| min, max:  1 1  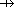  |
 |
 |
 |
 |
 |
| 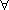 a,b: a,b:   a .. b = { i: a .. b = { i:  | a | a  i i  b } b } |
|  |
|  ... predicates for other operators omitted ... ... predicates for other operators omitted ... |
 |
Glossary
X 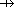 Y Y | - | Partial function: some members of X are paired with a member of Y |
X  Y Y | - | Total function: every member of X is paired with a member of Y |
X 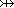 Y Y | - | Partial injection: some members of X are paired with different members of Y |
X 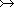 Y Y | - | Total injection: every member of X is paired with a different member of Y |
X 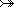 Y Y | - | Bijection: every member of X is paired with a different member of Y, |
| | covering all Y's |
Definitions
X 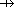 Y == { f: X Y == { f: X  Y | Each member of X appears no more than once. } Y | Each member of X appears no more than once. } |
 |
X  Y == { f: X Y == { f: X 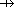 Y | dom f = X } Y | dom f = X } |
 |
X 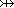 Y == { f: X Y == { f: X 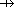 Y | Each member of X is paired with a different member of Y. } Y | Each member of X is paired with a different member of Y. } |
 |
X 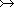 Y == (X Y == (X 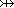 Y) Y)  (X (X  Y) Y) |
 |
X 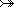 Y == ... definition omitted ... Y == ... definition omitted ... |
Glossary
| seq X | - | Sequence: the set of all sequences of X's |
| seq1 X | - | Non-empty sequence: the set of all sequences of X's |
| | with at least one element |
| iseq X | - | Injective sequence: the set of all sequences of X's |
| | where each element of X appears only once |
s 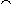 t t | - | Concatenation: sequence s with sequence t appended |
| head s | - | Head: the first element of sequence s |
| last s | - | Last: the last element of sequence s |
| front s | - | Front: all but the last element of sequence s |
| tail s | - | Tail: all but the first element of sequence s |
| s in t | - | Segment relation: the sequence s appears in sequence t |
Definitions
seq X == { f: 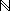 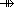 X | dom f = 1 .. # f } X | dom f = 1 .. # f } |
 |
| seq1 X == { f: seq X | # f > 0 } |
 |
iseq X == seq X  ( (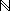 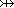 X) X) |
 |
| [X] |
 |
|
 |
 |
 |
 |
 |
 |
 |
 |
| head, last : seq1 X  X X |
| tail, front : seq1 X  seq X seq X |
| _ 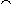 _ : seq X _ : seq X  seq X seq X  seq X seq X |
| _ in _ : seq X  seq X seq X |
 |
 |
 |
 |
 |
| 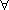 s: seq1 X; u,v: seq X s: seq1 X; u,v: seq X  |
|  |
|  head(s) = s(1) head(s) = s(1)  |
|  |
|  last(s) = s(# s) last(s) = s(# s)  |
|  |
|  u u 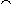 v = u v = u 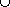 { i: dom v { i: dom v  i + #u i + #u 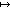 v(i) } v(i) } |
|  |
|  u in v u in v  ( (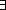 s,t: seq X s,t: seq X  s s 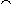 u u 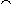 t = v) t = v) |
|  |
|  ... predicates for other operators omitted ... ... predicates for other operators omitted ... |
|  |
 |
 |
Z examples in web pages.
Z2HTML tool for translating
LaTeX documents with Z markup to HTML web pages.
Z home page
with FAQ and links to publications, tools, and meetings.
Back to top
Jonathan Jacky /
Department of Radiation Oncology
Box 356043
University of Washington /
Seattle, Washington 98195-6043 / USA
Tel (206) 598-4117 / Fax (206) 598-6218
E-mail: jon@u.washington.edu
![]() and this X are
about the same size:
and this X are
about the same size: ![]() X. See these viewing tips.
X. See these viewing tips.
![]() by X
by X ![]() Y ==
Y == ![]() (X
(X ![]() Y).
Y).
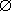
S
T
T
T
T
[X] == { x: X | false }
_ : X

X
_, _
_ :
X

X
_ , _
_, _ \ _:
X

X

X
x: X; S, T:
X

x
S

(x
X)
(S
T
(
x: X
x
S
x
T))
(S
T
S
T
S
T)

S
T = { x: X | x
S
X
T }

S
T = { x: X | x
S
X
T }

S \ T = { x: X | x
S
X
T }
y
Y
Y ==
(X
Y)
x
x }
Y
X
Y
Y
_ : X
Y
X
Y
Y)

X
Y)

Y
x: X; y: Y; R: X
Y

first(x,y) = x
second(x,y) = y
x
y = (x,y)
dom R = { x: X; y: Y | x R y
x }
ran R = { x: X; y: Y | x R y
y }
R
T
R
T
S
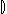
Q
_, _
_ :
X
(X
Y)
X
Y
_, _
_ : (X
Y)

Y
X
Y
Y)
(Y
X)
_
: (X
Y)

X

Y
_ : (X
Y)
(X
Y)
(X
Y)
X)
(X
X)
x: X; y: Y; S:
X; T:
Y; Q, R: X
Y

S
R = { x: X; y: Y | x
S
x R y
x
y }
S
R = { x: X; y: Y | x
S
x R y
x
y }
R
T = { x: X; y: Y | x R y
y
T
x
y }
R
T = { x: X; y: Y | x R y
y
T
x
y }
R ~ = { x: X; y: Y | x R y
y
x }


R
S
= { x: X; y: Y | x
S
x R y
y }
Q
R = ((dom R)
Q)
R
... predicate for _ + omitted ...
R
Q
R
_ : (X
Y)
(Y
Z)
(X
Z)
_ : (Y
Z)
(X
Y)
(X
Z)
Q: X
Y; R: Y
Z

Q
R = R
Q = { x: X; y: Y; z: Z | x Q y
y R z
x
z }

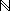
1


1
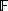
]
== { n:
| n
0 }
1 ==
\ { 0 }
1 X == { S:
X | S

}
X == { S:
X | ... S is finite ... }






(
\ { 0 })





_, _
_, _ > _ :









X

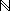
1

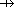
a,b:

a .. b = { i:
| a
i
b }
... predicates for other operators omitted ...
Y
Y
Y
Y
Y
Y == { f: X
Y | Each member of X appears no more than once. }
Y == { f: X
Y | dom f = X }
Y == { f: X
Y | Each member of X is paired with a different member of Y. }
Y == (X
Y)
(X
Y)
Y == ... definition omitted ...
t
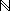
X | dom f = 1 .. # f }
(
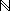
X)
X
seq X
_ : seq X
seq X
seq X
seq X
s: seq1 X; u,v: seq X


head(s) = s(1)
last(s) = s(# s)
u
v = u
{ i: dom v
i + #u
v(i) }
u in v
(
s,t: seq X
s
u
t = v)
... predicates for other operators omitted ...