BEE 531 Ultrasound beams
Instructor: Matthew Bruce / mbruce@uw.edu
University of Washington
Acoustic Beams
- How do we control/direct ultrasound.
- Wave equation.
- Integral solutions to the wave equation.
- Time/Frequency domain solutions.
- Some examples and simple simulations.
Why do we care about controlling where our ultrasound goes?
- Determines our lateral resolution.
- Determines depth of field.
- Reducing off-axis artifacts.
- Reduces reverberation artifacts.
Foundation of transmit and receive components of ultrasound imaging.
Ultrasound Image artifacts.Ultrasound artifacts
Sound Beams
- In ultrasound beams are used to guide waves to interact with our medium.
- A sound beam is bounded in 2 dimensions (x,y) and propagates in a third (z).
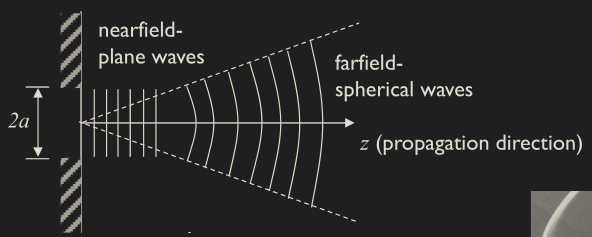

Diffraction
- Diffraction is how waves spread around a edge pass through an aperture.
- The abrupt edge of a radiation source like the edge of a piston.
- For arrays, diffraction describes how the sampling of the aperture affects the beam.
- Involves constructive and destructive interference of waves generated at the boundary of the source/obstacle.
- Scattering is typically refered to as diffraction of objects on the order and less than a wavelength.
Point Source
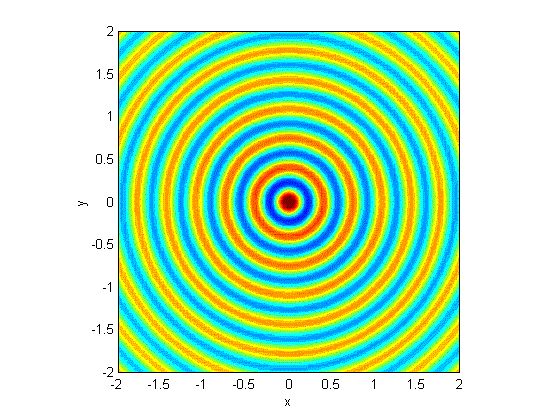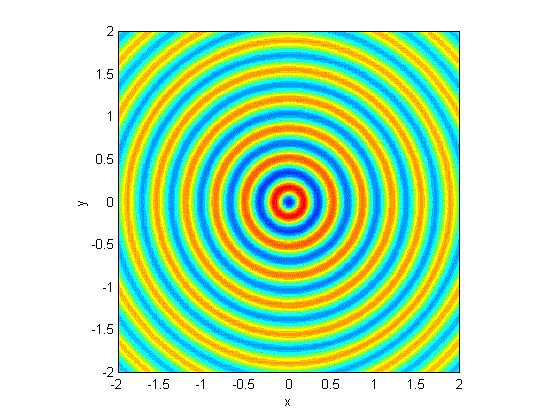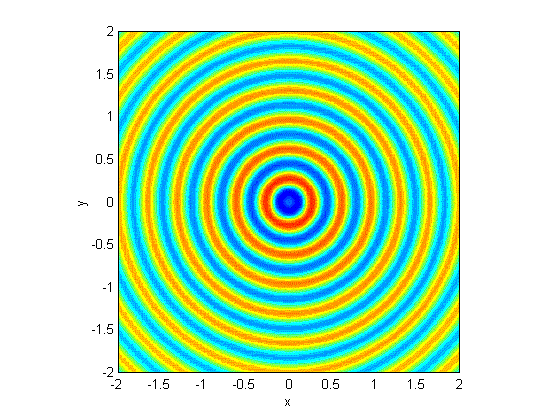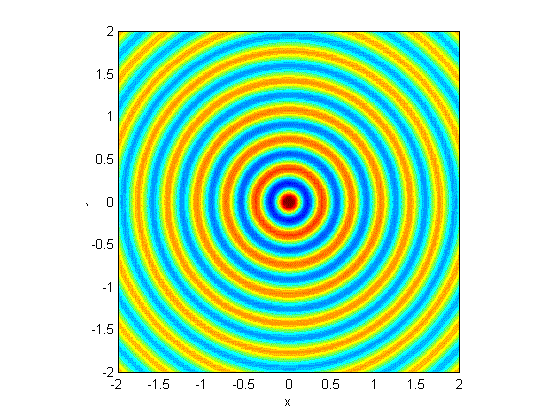
Point source/wave eq solved in spherical coord's. Link
Superposition/Interference
Two propagating waves results in
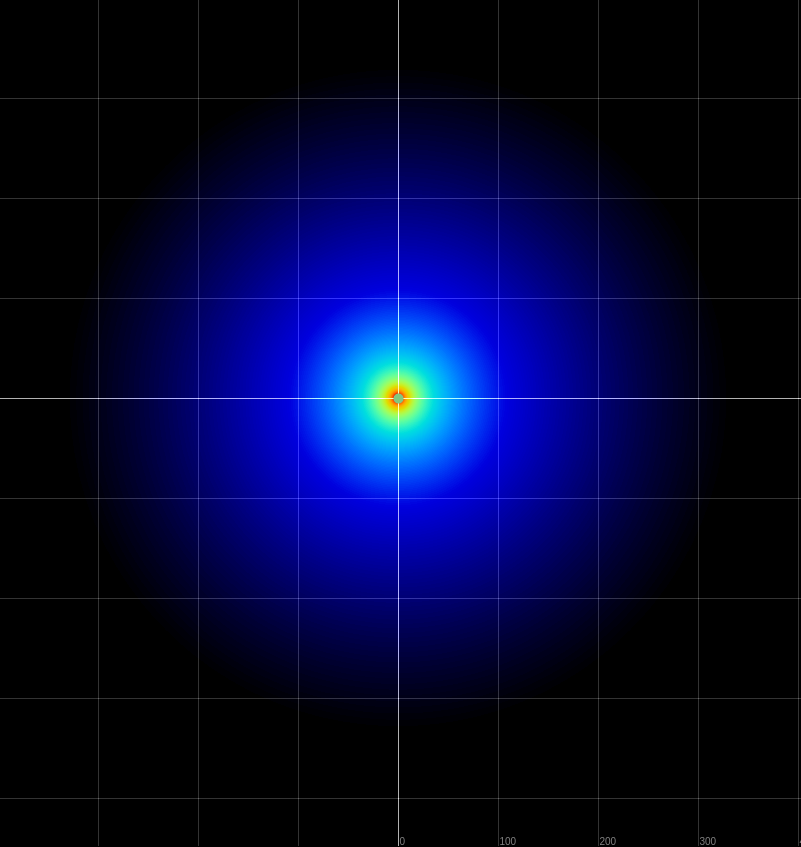
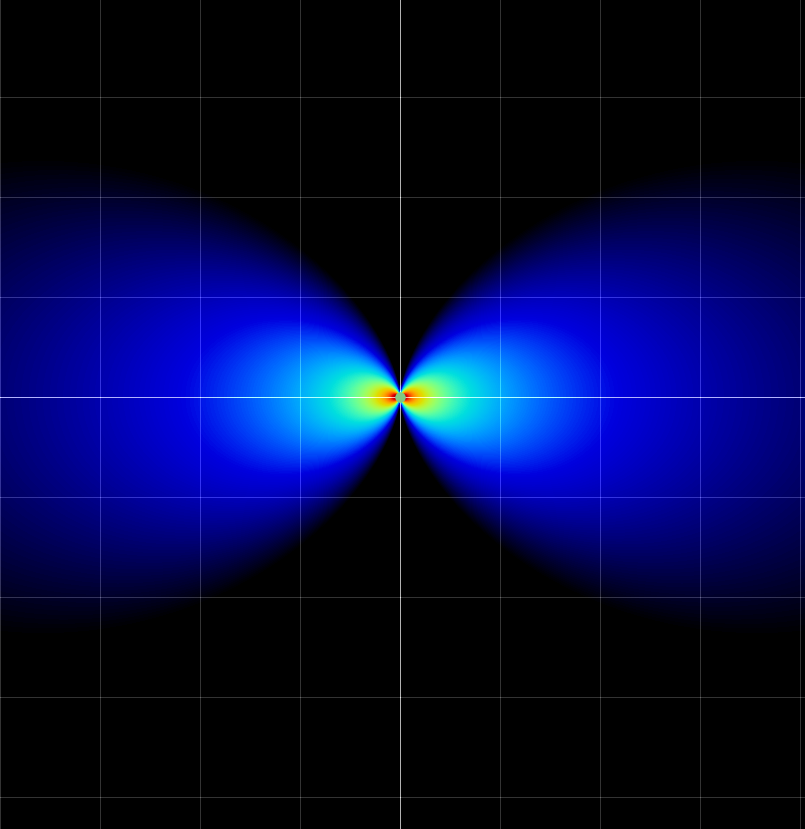
results in the sum of the two waves.
Simplified wave equations
Propagation in a homogeneous medium with compressibility \( \kappa \), shear and bulk viscosity \( \mu , \mu_B \), \( \mathbf{v}(\mathbf{r},t) = \nabla \phi(\mathbf{r},t) \):
\( \nabla^2 \phi + \kappa(\mu_B+\frac{4}{3} \mu) \frac{\partial}{\partial t} (\nabla^2 \phi) = \kappa \rho_0 \frac{\partial \phi}{\partial t^2} \\ \)- Small amplitude compressional wave.
- An irrotational vector field can be described by \( v = - \nabla \phi \)
- \( \mu = \mu_B = 0 \quad (\textrm{no shear and bulk viscosity})\).
- \( c_0 = \frac{1}{\sqrt{\kappa \rho_0}}= \sqrt{\frac{B}{\rho_0}} \).
- \( v = - \nabla \phi, \; p= \rho \frac{\partial \phi}{ \partial t} \).
Solving the wave equation
- Analytic approaches
- Limited to simple scenarios.
- Solving Greens function for geometry.
- Eg. piston, rectangular sources.
- Numerical approaches
- Most often used (FEM, FD, angular spectrum).
- Eg. Fields II, k-wave, MUST, Focus, ...
- Large numerical packages: Comsol, etc..
Simplified analytic wave solutions
- Solve Greens function/impulse response.
- Geometry is flat source into free space.
- Sometimes leading to Rayleigh integral.
- Time and frequency domain approaches.
- eq. (2) sum of point sources over source surface.
Analytic wave solutions
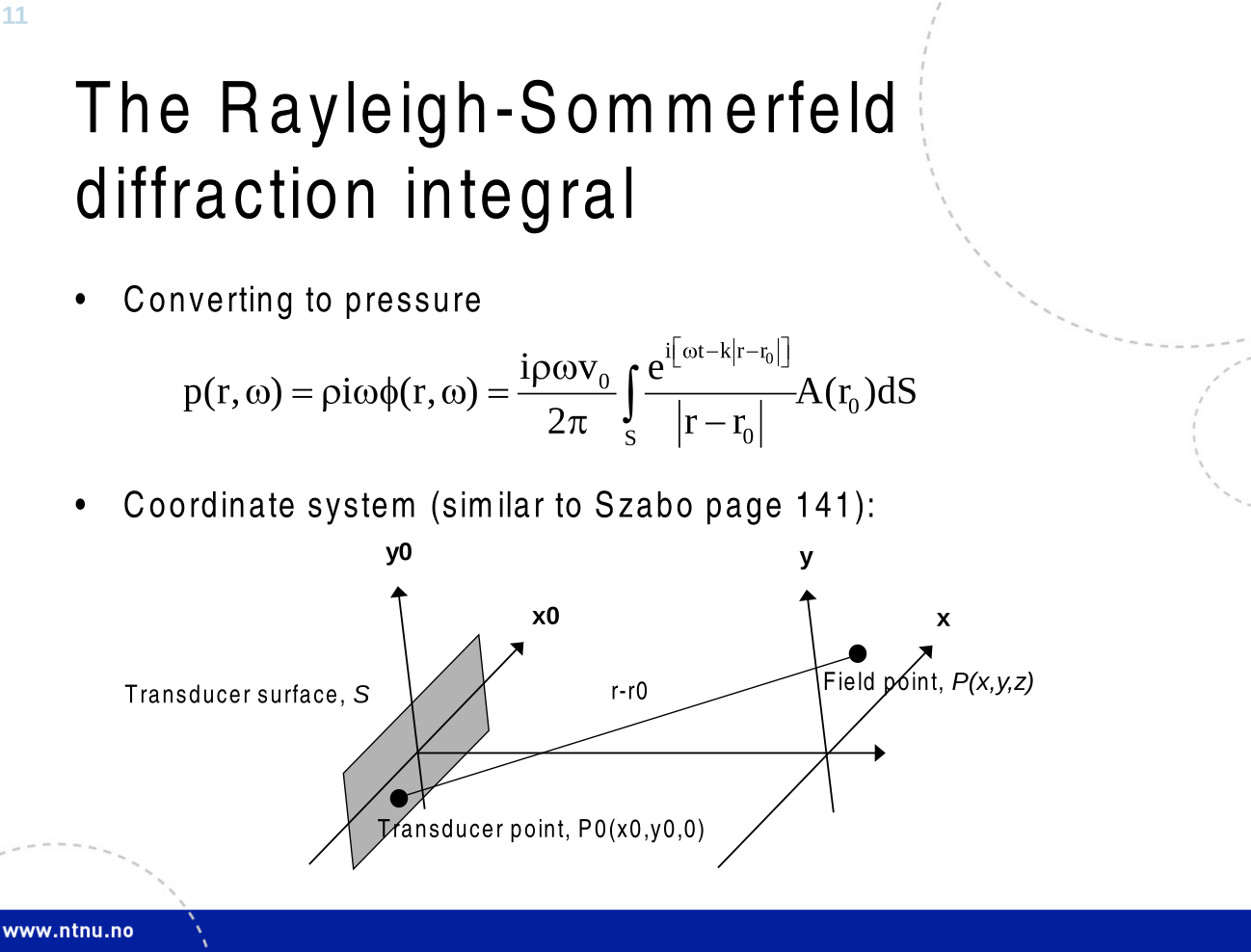
Rayleigh-Sommerfeld diffraction equations:
\[ \Phi(\mathbf{r}, \omega) = \frac{1}{2 \pi} \iint\limits_{S_0} \frac{e^{-jkR}}{R} \frac{\partial \Phi}{\partial n} \, dS_0 \; (1) \\ \\ \phi(\mathbf{r}, t) = \frac{1}{2 \pi} \iint\limits_{S_0} \frac{v_n(t-\frac{R}{c})}{R} dS_0 \; (2) \]- All of the assumptions above plus:
- Geometry is flat source into free space.
- eq. (1) For a single frequency sum of point sources over source surface.
- eq. (2) Time domain point sources over source surface.
The Rayleigh Integral
Can be expressed as convolution (\( v_n(x,y,0,t)=A(x,y)v_n(t)\)): \[ \phi(\mathbf{r}, t) = \frac{1}{2 \pi} \iint\limits_{S_0} \frac{v_n(t-\frac{R}{c})A(x_0,y_0))}{R} dS_0 \; (2) \quad v_n(t-\frac{R}{c}) = \int\limits_{\infty}^{-\infty} v_n(\tau) \delta(t-\frac{R}{c}-\tau) d\tau \] \[ \phi(\mathbf{r}, t) = \int\limits_{\infty}^{-\infty} v_n(\tau) \color{orange}{\iint\limits_{S_0} \frac{A(x_0,y_0) \delta(t-\frac{R}{c}-\tau))}{R} dS_0}d\tau \]
- \( \phi(\mathbf{r}, t)=v_n(t) \ast \color{orange}{h(r,t)} \)
- \( v = - \nabla \phi, \; p= \rho \frac{\partial \phi}{ \partial t} \).
- \( p(r,t)= \rho v_n(t) \ast \frac{\partial h(r,t)}{ \partial t} \).
- \( v(r,t) = -v_n(t) \ast \nabla \color{orange}{h(r,t)} \).




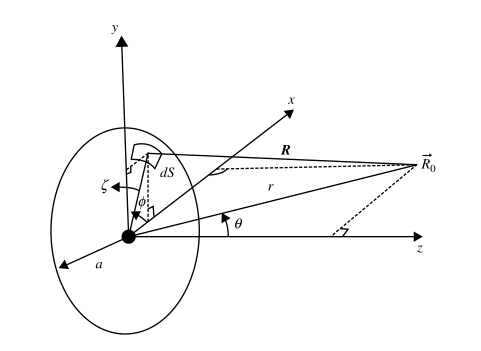
Unfocused piston
\( \nabla^2 P - \frac{\partial P}{\partial t^2} = f(\mathbf{r},t) \\ \)
\( P(\mathbf{r}) = - \frac{jk \rho_0 c}{2 \pi }\int\limits_{S_0} \frac{e^{-jkR}}{R} U_n \, dS_0 \; \\ \)
\( P(r,\theta) = - jk \rho_0 c U_n \frac{e^{jkr}}{r} a^2 \frac{J_1(ka sin \theta)}{ka sin \theta } \\ \)
Unfocused piston: on axis
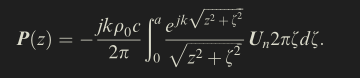
\( P(z,0) = \rho_0 c U_0 (e^{jkz} - e^{jk \sqrt{z^2 + a^2}}) \)
\( P(z,0) = \rho_0 c U_0 (1 - e^{-j k ( \sqrt{z^2 + a^2}-z)} ) \)
\( P(z,0) = 2 \rho_0 c U_0 (sin( \frac{kz}{2} [\sqrt{1 + (\frac{a}{z})^2 } - 1])) \\ \)
If z>>a then the magnitude of field looks like from a point source:
\( P(z,0) \approx 2 \rho_0 c U_0 sin( \frac{ka}{4} \frac{a}{z} ) \approx \frac{1}{2} \rho_0 c U_n ka \frac{a}{z} \\ \)
Unfocused piston: transverse field
\( P(r,\theta) = - jk \rho_0 c U_n \frac{e^{jkr}}{r} a^2 \frac{J_1(ka sin \theta)}{ka sin \theta } \\ \)
\( P(r,0) = - j \rho_0 c \frac{k a^2}{r} e^{jkr} \frac{U_n}{2 } \\ \)
\( P(r,\theta) = P(r,\theta) 2 \frac{J_1(ka sin \theta)}{ka sin \theta } \\ \)
refs: Kinsler-Fund Acoustic waves and Kim-Sound Prop Imp
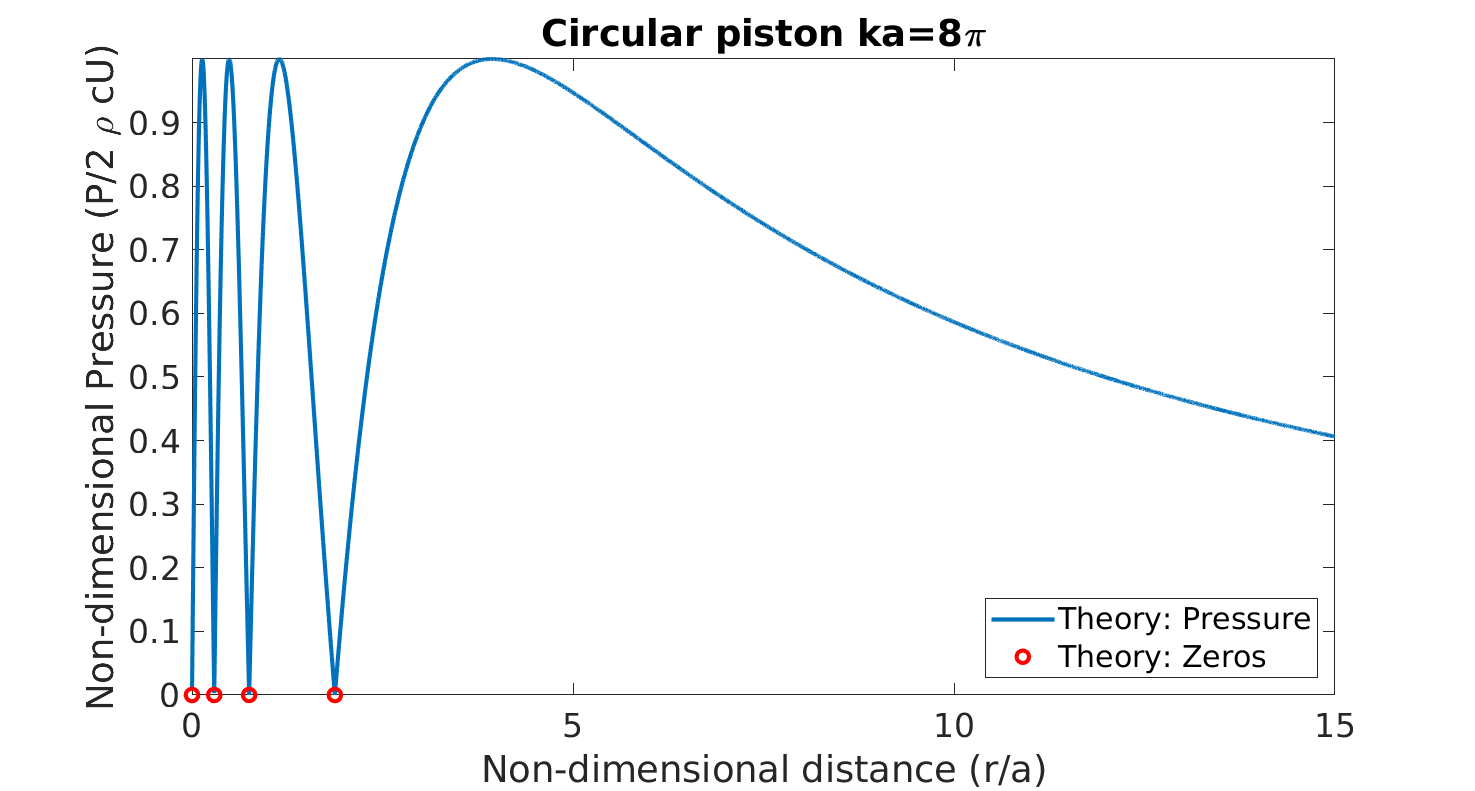
Unfocused piston: on axis

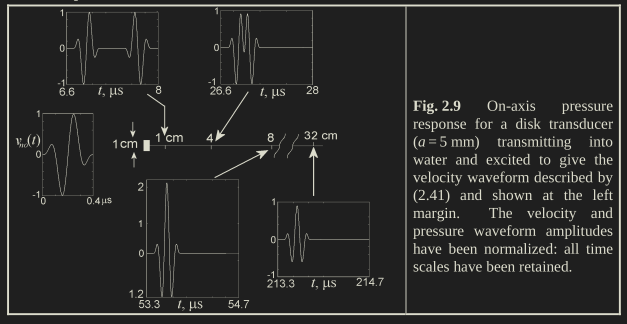
Sourse: Foundations in Biomedial Ultrasound by Cobbold
Simple numerical solution to Rayleigh-Sommerfeld equation
\[ p(\mathbf{r}, \omega) = \frac{i\rho \omega v_o}{2 \pi} \iint\limits_{S_0} \frac{e^{-jkR}}{R} A(x_0,y_0) \, dS_0 \]
for m=1:100
for l=1:100
pt(l,m)=0;
psum=0;
for nrad=1:36
sgma=nrad*a/36;
for nang=1:36
psi=nang*2*pi/36;
zs=sgma*cos(psi);
ys=sgma*sin(psi);
rp=sqrt((zs)^2+(y(l)-ys)^2+x(m)^2);
dp=exp(-i*k*rp)/rp*sgma;
psum=psum+dp;
end
end
pt(l,m)=psum;
end
end
Homework 2, problem 3: Purdue ME 513 Engineering Acoustics. Link
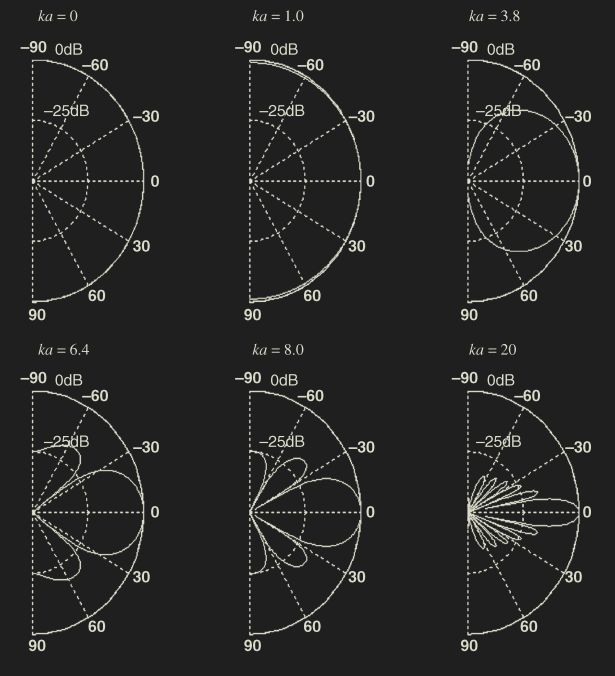
Piston increasing ka
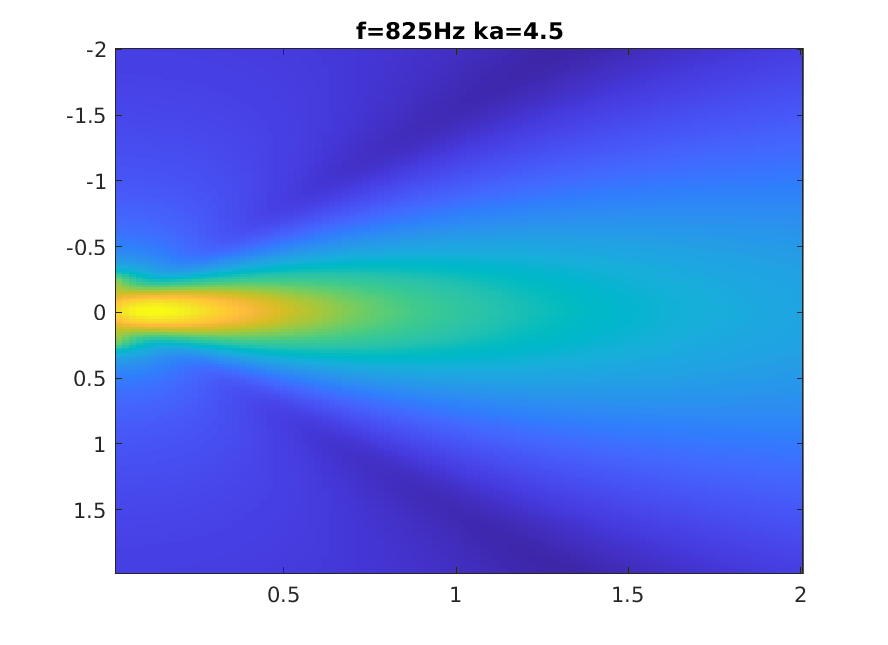
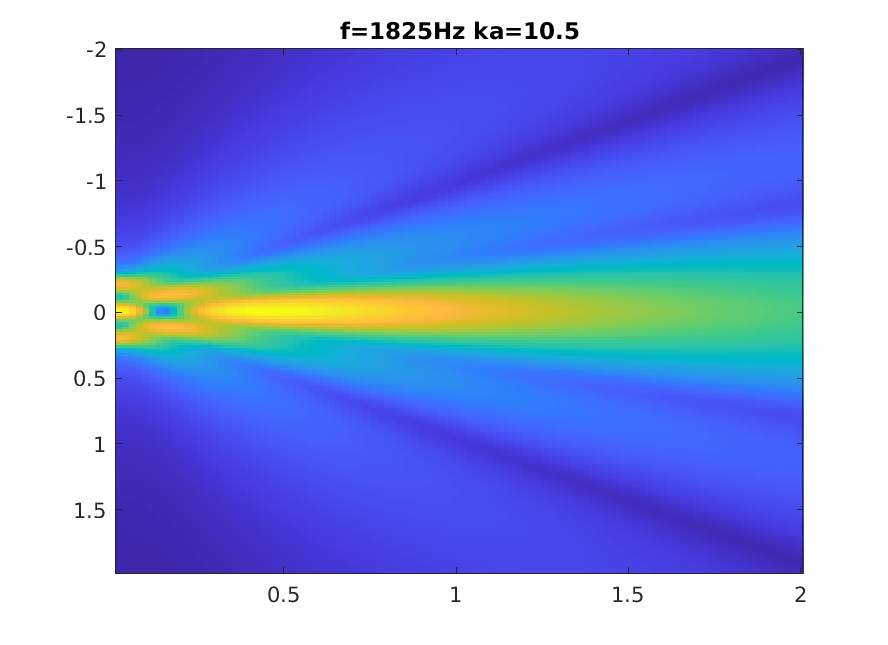
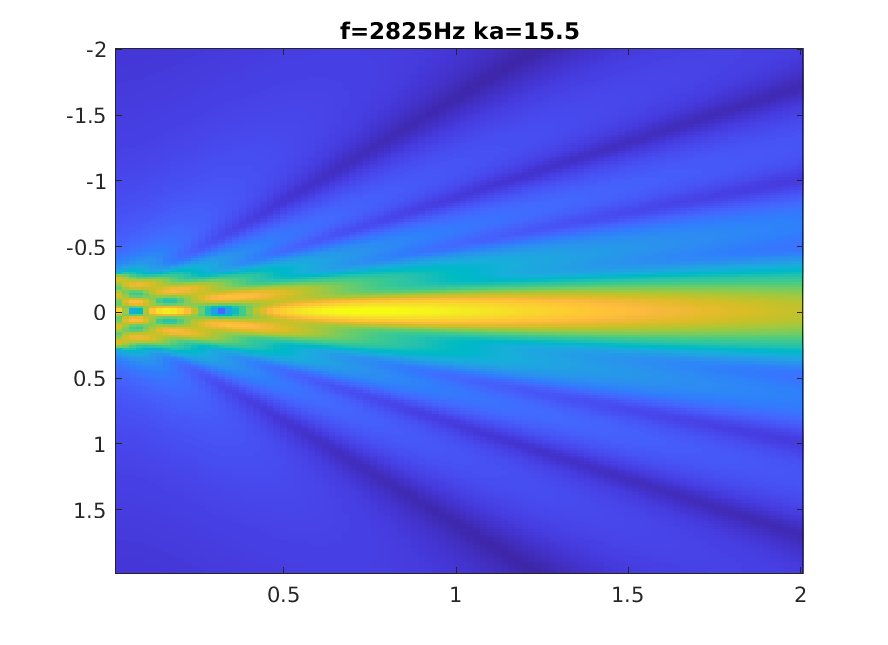
Numerical calculation of Rayleigh integral.
Piston increasing ka
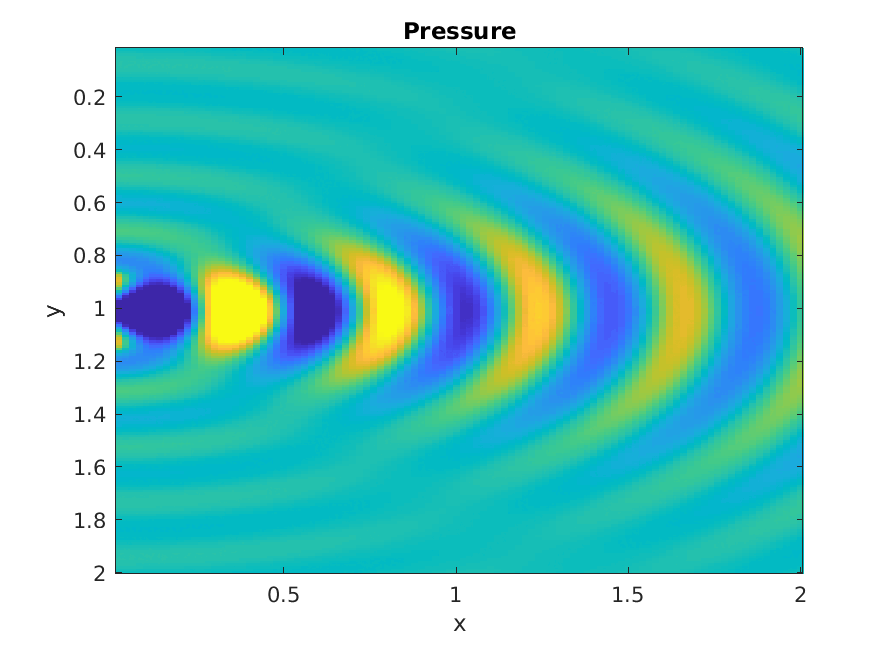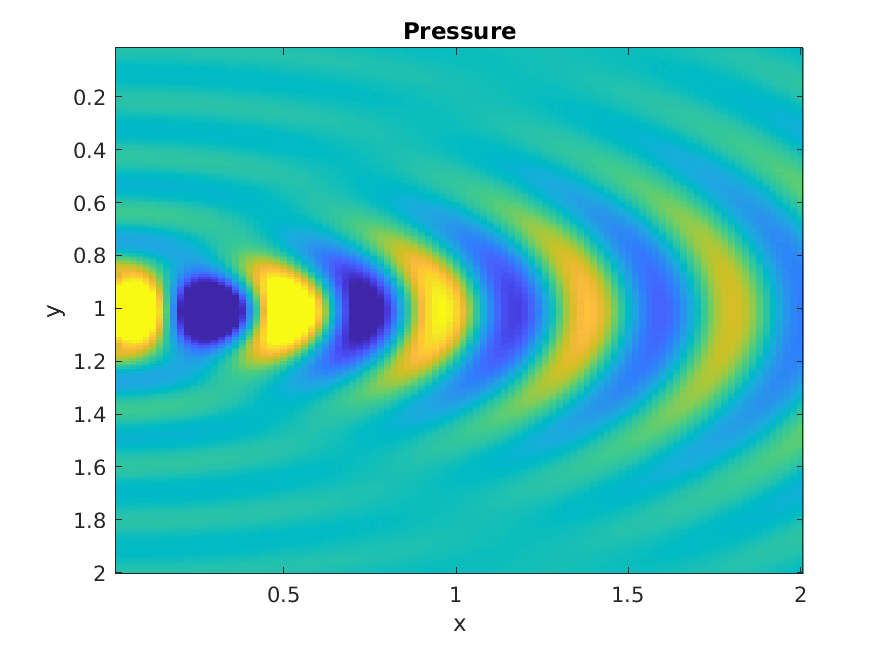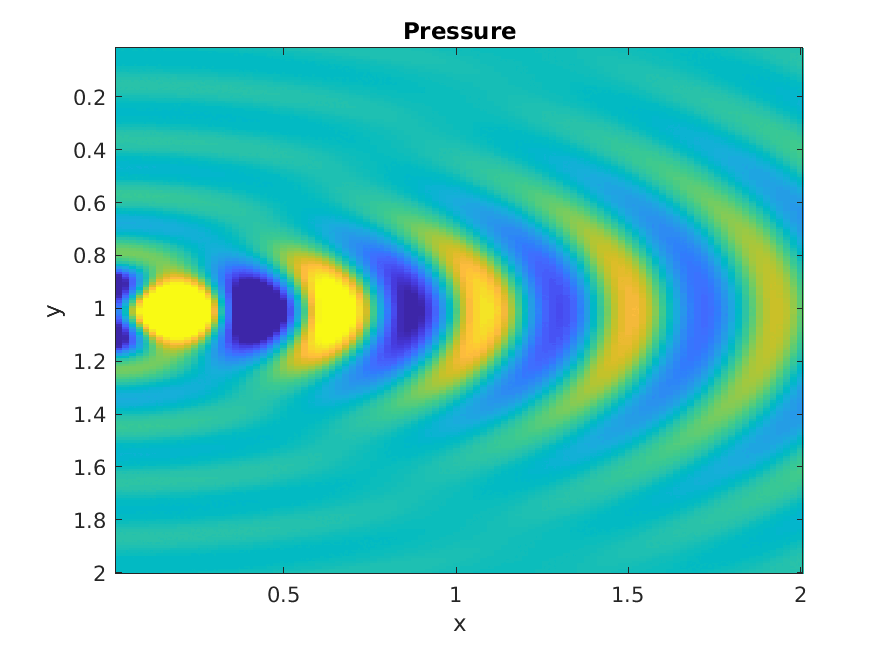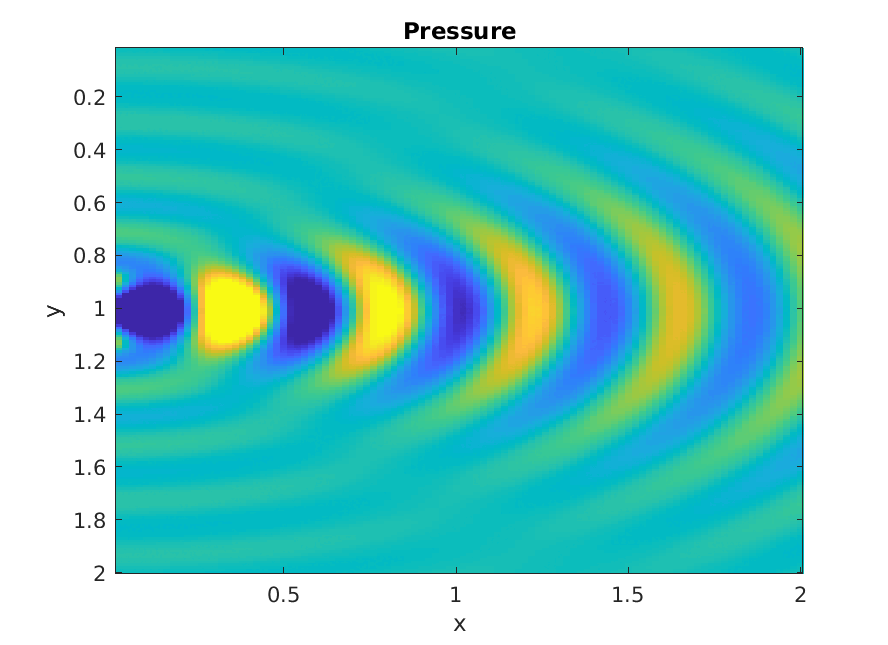
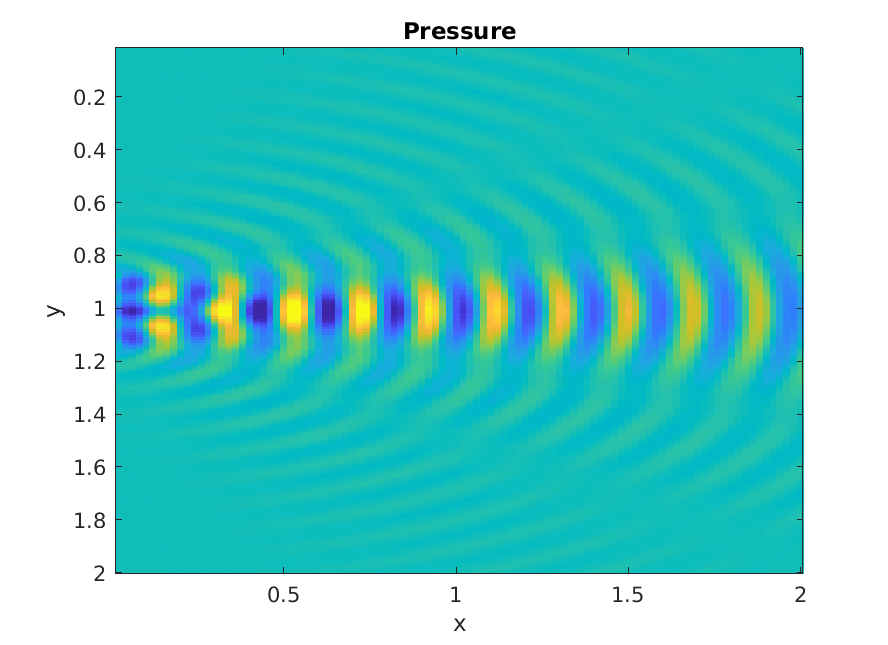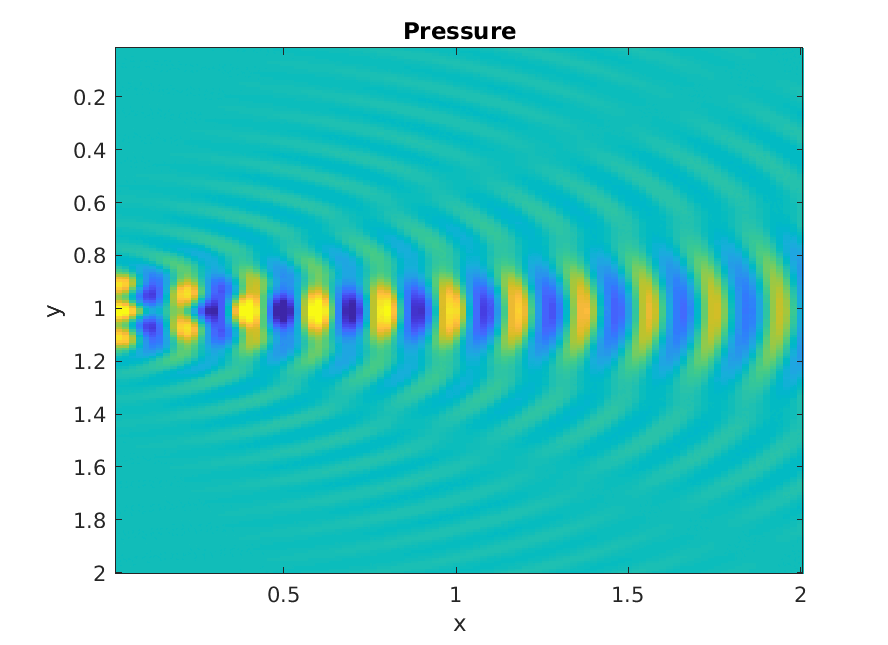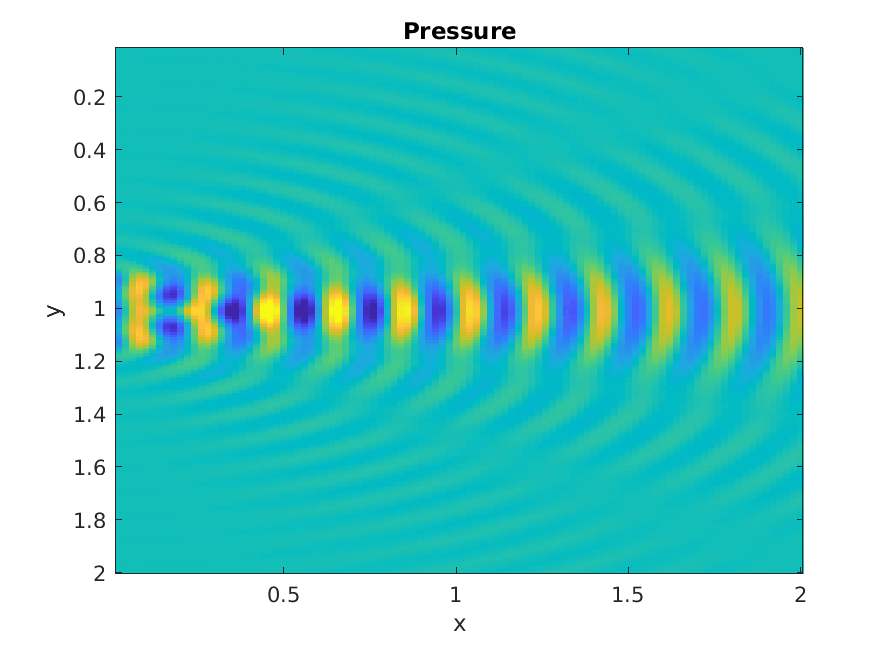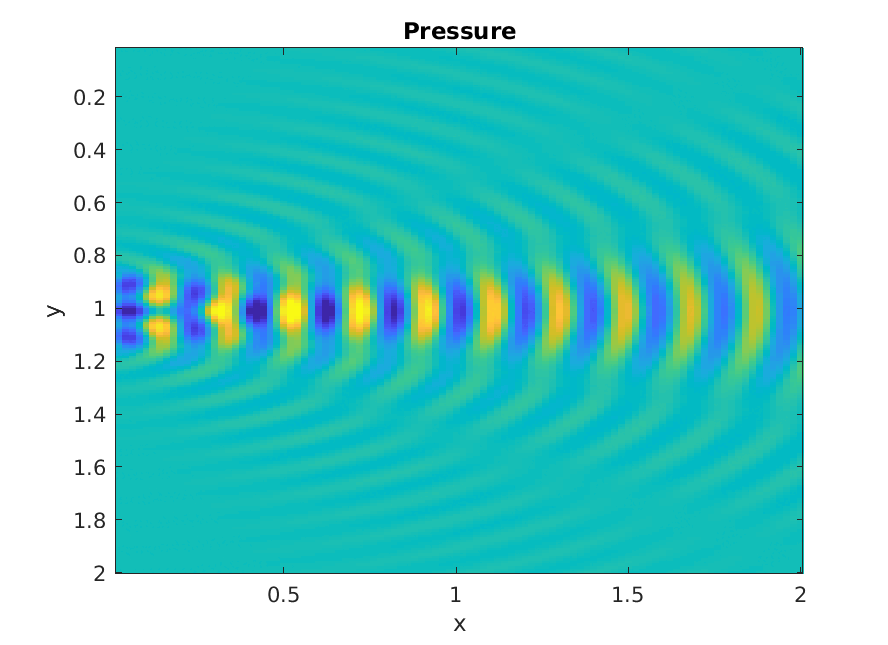
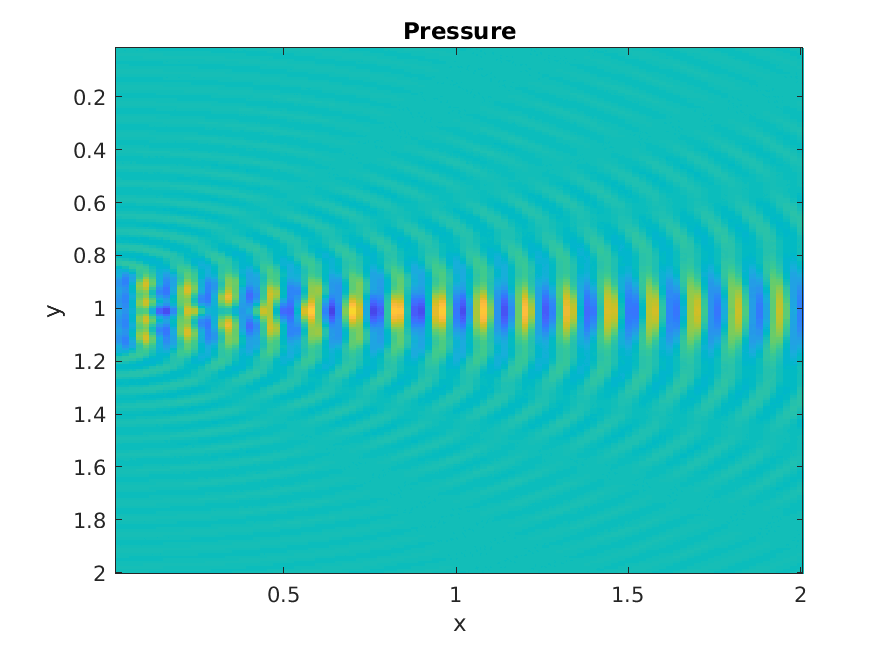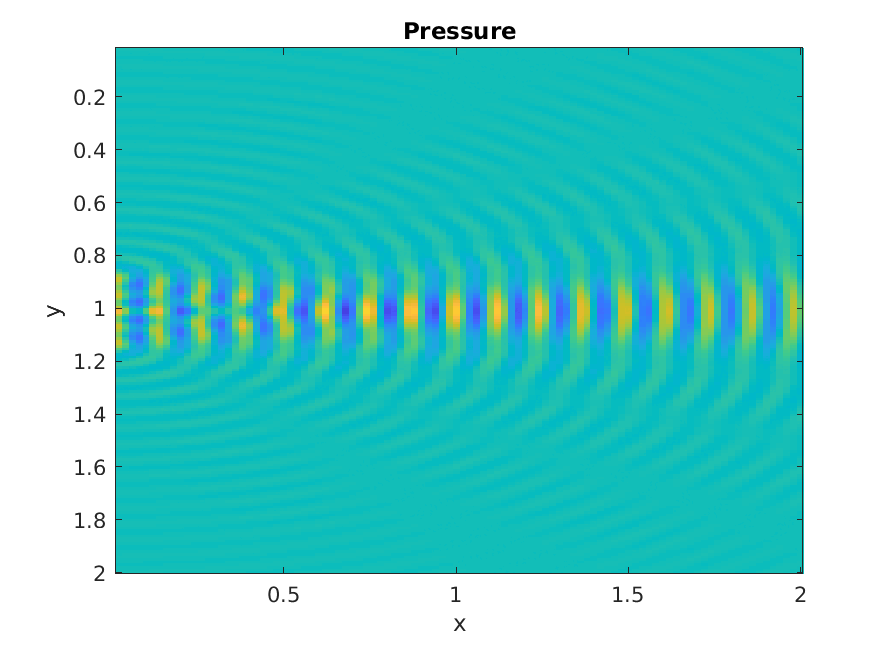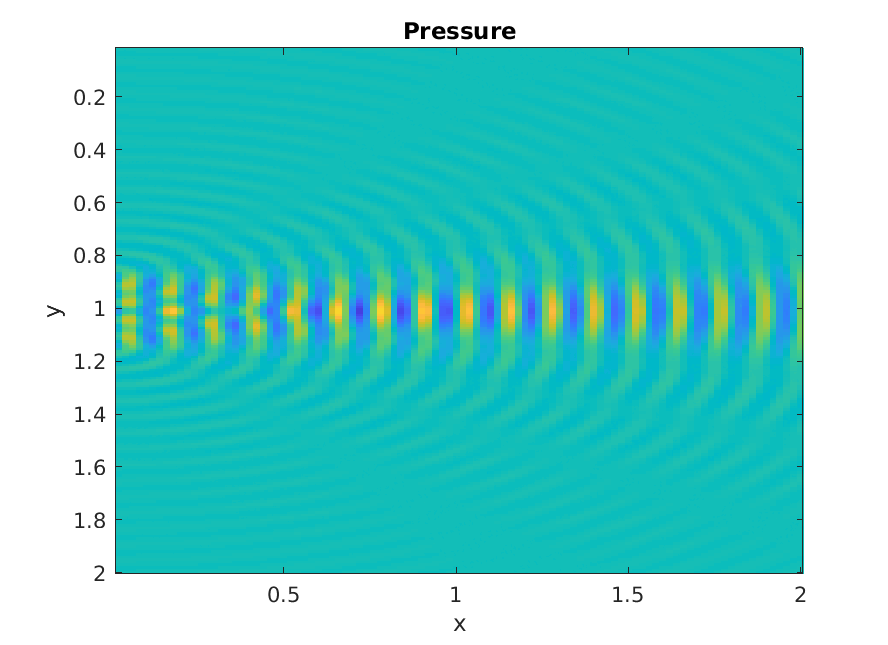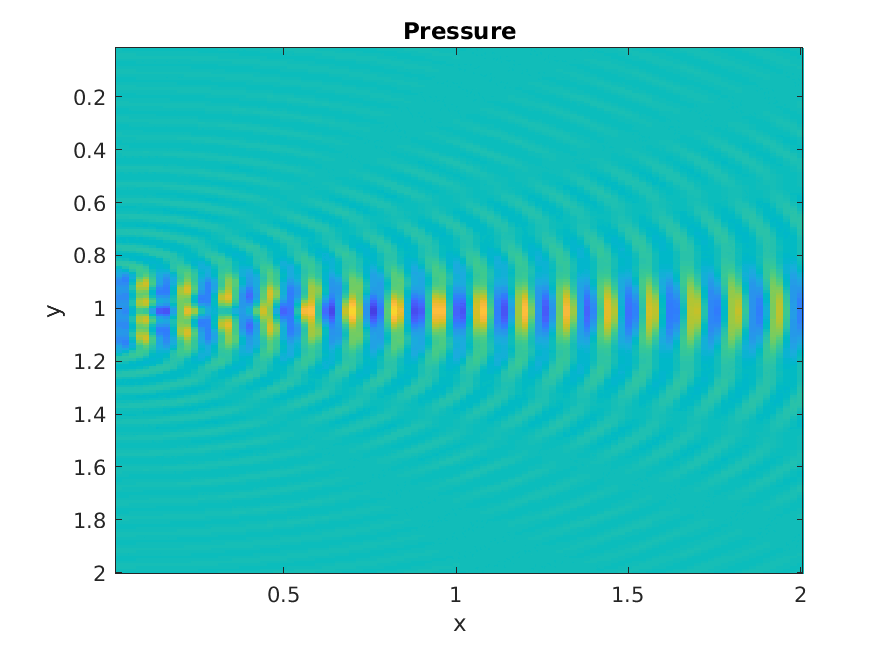
Numerical calculation of Rayleigh integral.
Focused beams
Sound beams for biomedical applications
- Size: 1-10 cm dia or side, 1-20 cm focus
- Frequencies: 0.5-10 MHz.
- Medium: blood, soft tissues.
- Density: 1000 kg/m^3
- Speed of sound: 1500 m/s.
- Attenuation: ~0-1 dB/cm/MHz .
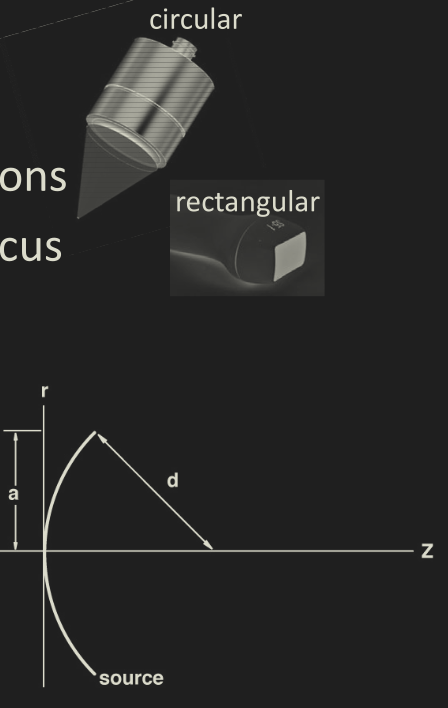
Focused beams
- Focusing implemented with either curved transducers, a lens, or electronics delays
- Focusing gain: pressure at focus dividied by the pressure at the source.
- \( G = \frac{p(x=d)}{p(x=0) }=\frac{ka^2}{2d} \)
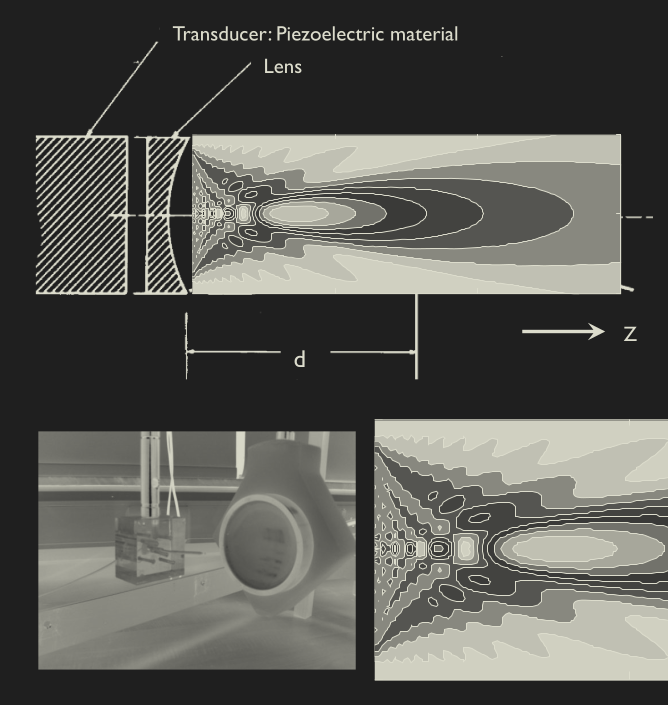
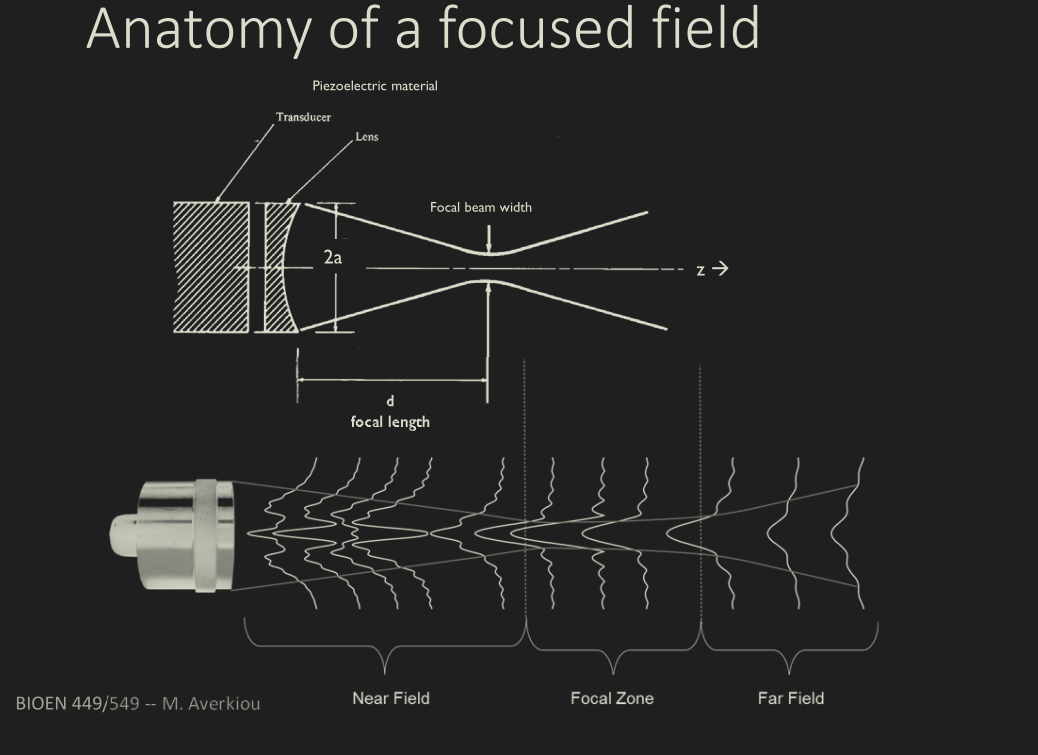
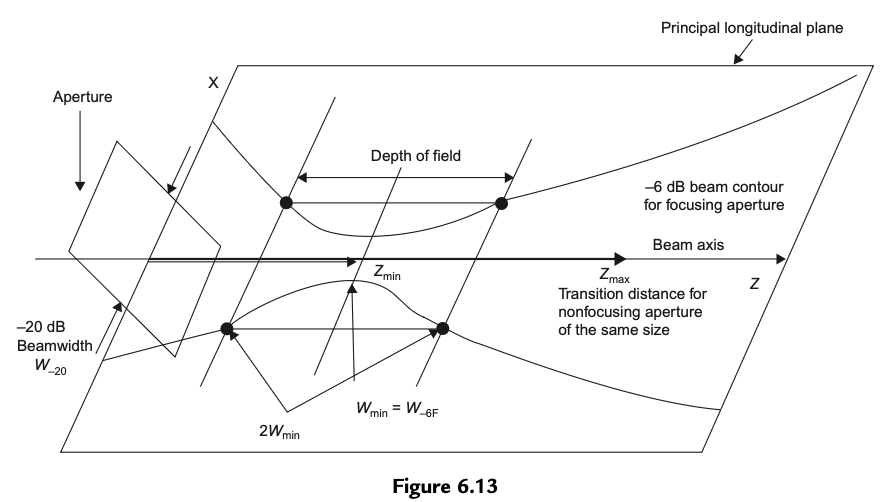


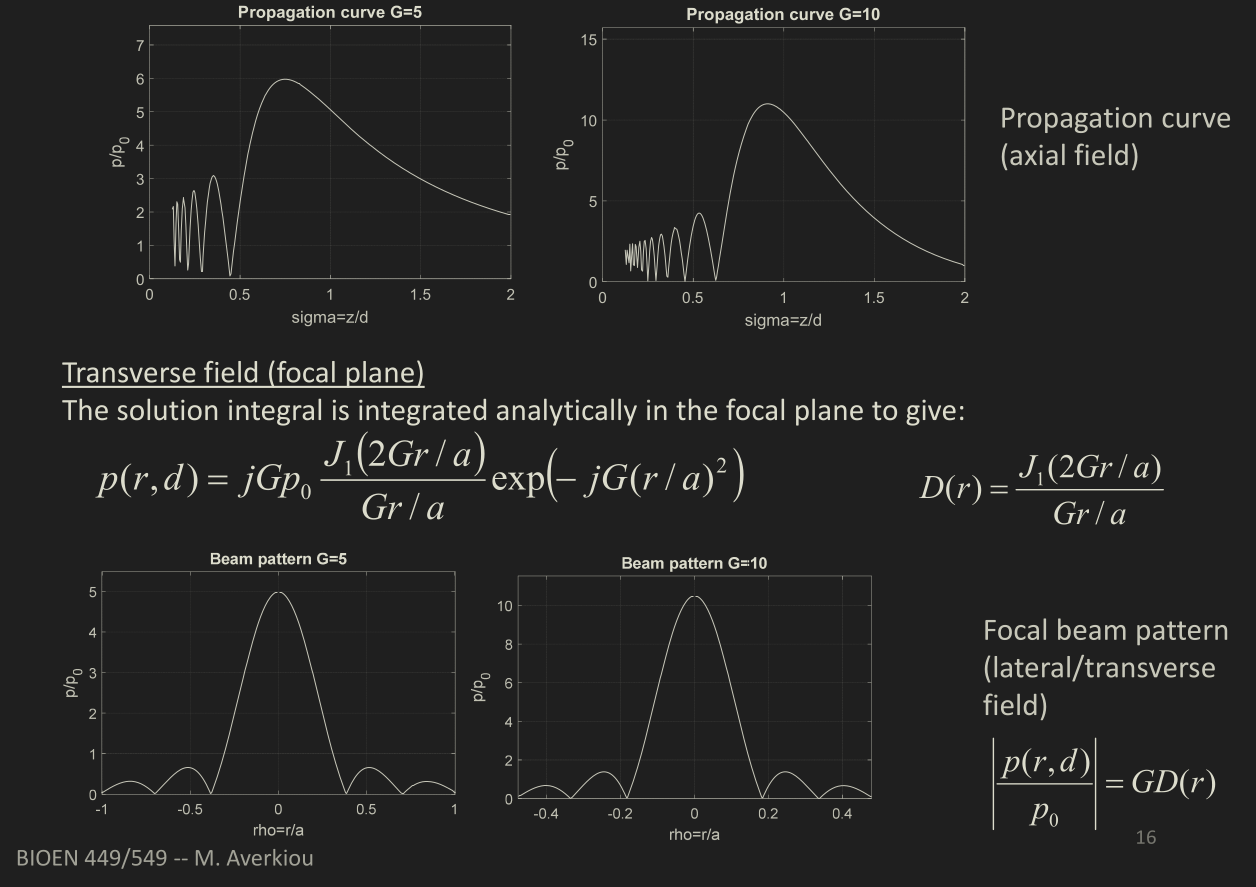

Unfocused beams
Near field directing of beam:
Focused beams
Shallow focus:
Focused beams
Deeper focus:
Single slit diffraction pattern (rectangular aperture)
\( P(r) = A(r)e^{j \omega t} (e^{j k r_1} + e^{j k r_2} + ... + e^{j k r_N}) \)
\( r_2 = r_1 + d \sin \theta \\ r_3 = r_1 + 2d \sin \theta \\ ... \\ r_N = r_1 + (N-1)d \sin \theta \\ \)
\( P(r) = A(r)e^{j \omega t} e^{j k r_1} S \)
\( S = 1 + e^{j k (r_2 - r_1)} + e^{j k (r_3 - r_1)} + ...\)
\( S = 1 + a + a^2 ... a^{N-1}\)
Single slit diffraction pattern (rectangular aperture)
\( S = 1 + a + a^2 ... a^{N-1} \)
\( a = e^{j k (r_2 - r_1)} = e^{jk \sin \theta}=e^{j \Delta \phi} \)
\( \Delta \phi = k d \sin \theta = \frac{2 \pi}{\lambda }d \sin \theta \)
\( aS - S = a^N - 1 \)
\( S = \frac{a^N-1}{a-1}\)

Single slit diffraction pattern (rectangular aperture)
\( aS - S = a^N - 1 \)
\( S = \frac{a^N - 1}{ a - 1} = \frac{e^{jN \Delta \phi} - 1}{ e^{j \Delta \phi} - 1} = \frac{e^{j(1/2)N \Delta \phi}}{e^{j(1/2) \Delta \phi}} \frac{e^{j(1/2)N \Delta} - e^{j(1/2)N \Delta}} {e^{j(1/2) \Delta} - e^{j(1/2) \Delta} } \)
\( S = e^{jN \Delta \phi} \frac{\sin \frac{1}{2} N \Delta \phi}{\sin \frac{1}{2} \Delta \phi} \)
\( N \to \infty, \; \; \; \Phi =(N-1)\Delta \phi = kD \sin \theta \)
\( \Phi \approx N \Delta \phi \)
\( S = \frac{\sin \frac{1}{2} \Phi}{\sin \frac{1}{2} \Phi / N}= \frac{\sin \frac{1}{2} \Phi}{\frac{1}{2} \Phi } \; \; \; \; \Phi = 2 \pi \frac{D \sin \theta}{ \lambda }\)
\( \Delta \theta = \frac{\lambda}{D} \)