Keywords: attribute error, positional error, confusion matrix, categorical map, polygon overlay

Abstract

A test designed to distinguish positional error from attribute error, posited by Chrisman and Lester (1991), is applied to overlays of two old growth forest datasets. These datasets are more complicated and cover far more acreage than previous applications of the test. In the test, polygons whose boundaries are equally derived from the two different source layers are identified as positional error. The results of the error analysis show that positional and attribute errors clearly are drawn from different populations. Because the two types of errors have different sources and have different implications, it is useful to distinguish between the two.

Introduction

In 1989, two different projects set out to map old growth in the Pacific Northwest. Despite their identical goals, timeframes, definition of old growth and other similarities, they produced very different results. An examination of some of the differences that led to these results, and a closer review of the results, can be found in Norheim (1996, 1997).

In that analysis, however, no consistent trend was found in any of the disagreements between the two projects. Nevertheless, understanding the nature of error in a dataset is necessary before deciding to use a dataset for any given purpose (Goodchild and Gopal 1989). Because the stakes in the old growth controversy were so high, and because critical decisions were being made on the basis of these datasets, a full understanding of the error in them is particularly important.

One possible way to refine the analysis would be to better characterize some of the disagreement between the two studies. Congalton and Green (1993) identify several different sources of confusion, including registration errors, digitizing errors, interpretation error, temporal problems, and classification errors. Goodchild et al. (1992) proposes an error model for categorical data. Several papers suggest the use of fuzzy logic to better describe the boundaries between polygons (Lowell 1994, Lowell and Edwards 1994, Edwards and Lowell 1996). However, these procedures have limitations in many real world applications. Specifically, they require previous knowledge or assumptions about the nature of the error that is present, which is often not known.

In response to this problem, Chrisman and Lester (1991) propose a diagnostic test for error in an overlay of categorical maps, one which requires no previous knowledge of the nature of the error in the sources. The test examines the geometry and topology of an overlay, thus retrospectively making a categorization of the errors present in the overlay. The test distinguishes between errors that appear to arise from positional disagreement in the source layers versus errors that are likely to result from attribute disagreement, using decision rules that are based on experimental evidence regarding the relative geometry and topology of positional and attribute errors. Positional error is more likely to derive from the technology used, whereas attribute error is more likely to be a more substantive disagreement over the nature of the polygon in question (Chrisman 1989). As an example, Chrisman and Lester (1991) apply the test to two different interpretations of the same imagery.

This paper applies this test to the two old growth mapping projects, thus applying the test for the first time to two sources that are entirely independent of one another. It is the intention of this paper to gain further insight into the differences between the two old growth mapping projects by distinguishing positional from attribute error in an overlay of the two, thereby better informing our use of the two datasets.

Data Sources

In 1988, the National Forests in the Pacific Northwest were in the middle of the spotted owl controversy. The Forest Service was logging old growth forest at increasing rates. However, old growth forest was the only habitat for the spotted owl, which was on its way to the endangered species list as a result of the logging. A critical factor in the ensuing negotiations was how much old growth acreage was left (Hirt 1994, Yaffee 1994). Environmental groups raised serious doubts as to how accurate the U.S. Forest Service (USFS) acreage totals for old growth forest were. As a result, Congress directed the Forest Service to inventory its old growth (Congalton et al. 1993). Because of the tight deadline imposed by Congress, the agency turned to an outside consulting firm that used satellite imagery to complete the project (Norheim 1996, 1997).

The Wilderness Society began its own program of mapping old growth at about the same time (Morrison et al. 1991). While they used satellite imagery to determine recent clearcuts, the majority of the Society's old growth data for the forests in Washington State was from photo-interpretation. This was a much lengthier process than image processing, and the Society's team came under mounting pressure to increase the speed at which they completed their project. Hence, as they continued their photo-interpretation, they accelerated the pace of their work but thereby they decreased the confidence they had in it (Norheim 1996, 1997).

Norheim (1996, 1997) compares these two projects and examines their many similarities and differences. For the purposes of this paper, the two resulting datasets are ideal for the Chrisman and Lester test, because they are from entirely independent sources. While preferably for such a test we could assert that one or the other data source was "correct", Norheim came to no such conclusion in his comparison. Nevertheless, Chrisman (1989) states that a test for error in categorical maps could also be a test of repeatability. Indeed, we are most interested in the repeatability aspect in a test of the two old growth projects, because Norheim was unable to determine from a simple overlay that there was any systematic bias between the two datasets. Perhaps the diagnostic test can shed some light on the reasons for the differences in the two projects.

Note that this paper will continue to use the term 'error' when describing differences between the two datasets, as if one of them were correct, rather than a more unwieldy term such as 'disagreement' or 'confusion'.

Nature of old growth polygons. The errors that might occur in the boundaries surrounding old growth polygons in this region range from very sharp (where an old growth stand is adjacent to a clear-cut) to very fuzzy (as when an old-growth stand is adjacent to a slightly younger stand). Unfortunately, one of the projects used as a source in this study was strictly charged with distinguishing old growth without regard to neighboring stands. (A further study made these categorizations several years later) (Congalton et al. 1993). While a categorization of error based on fuzzy set theory (Lowell 1994) would be more satisfying, the limitations of the data sources preclude this option. Thus, the approach that is followed in this paper is simply an a posteriori categorization of the different categories of error. It is not an attempt to actually model the process from which the error was generated, but rather an exploratory characterization (Chrisman 1989).

The test

Space allows only a much-condensed description of the procedure of the test in this paper. The reader is referred to the original paper (Chrisman and Lester 1991) for a full description of the test and the rationale behind it.

The test involves six steps, and results in polygons being categorized in three ways. Polygons can either be not in error, or represent one of two kinds of error. Error can either be an attribute error, for example, one source has an island polygon of clearcut within an area both sources otherwise classify as old growth; or a positional error, for example, the two sources disagree on exactly where a clearcut polygon ends, resulting in a sliver polygon when overlaid.

The sequence of the test is shown in the flow chart in Figure 1. Step one asks whether there is indeed an error (e.g., are the attributes identical). The second step asks whether the boundaries are mostly coincident within a specified tolerance; if more than 85% of the linework agrees, the error must be an attribute error. In the tests applied for this paper, a tolerance of 3 meters was used; because the two sources were based on different grid sizes of 57 and 25 meters, virtually none of the linework agreed.

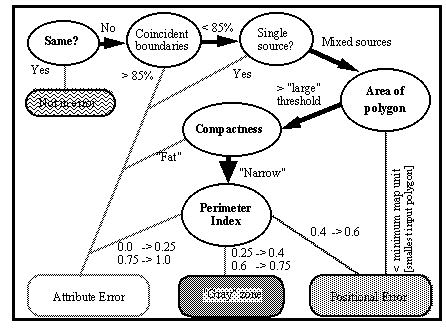
Figure 1 Flow of test applied to each overlay polygon
(Adapted from Chrisman and Lester 1991)

Step three looks at the source of the lines also; if all of the non-coincident lines of a polygon are from one source, then it is an island of a different attribute and not a case of partial overlap. The fourth step is to determine whether a polygon is smaller to a specified "minimum map unit", in which case the error is deemed to be positional as such a polygon is too small to come from the data sources. In the old growth application of the test, the minimum map unit is 5625 m2. This figure is equal to nine 25 m grid cells, which is the size of the filter applied when the Forest Service converted their pixel layers to polygons.

In step five, polygons that are relatively less compact are classified as attribute error if they are relatively large. To do this, compactness and "minimum compactness" values are calculated for each polygon. The compactness values are based on Unwin's S2 (1981). The minimum compactness is based on the minimum discrimination distance. Any polygon that is both larger than the square of the minimum discrimination distance and more compact than the minimum compactness is at once large enough and wide enough to have been identifiable in the source layers, so it is reckoned to be an attribute error.

In the sixth and final step of the test, a perimeter index is calculated for all polygons not previously classified. This index is a ratio of the perimeter from one source to the total of the non-coincident perimeter from both sources. Chrisman and Lester demonstrate that in a test where a source is shifted positionally and then compared to itself (thereby all error should be a positional error), the perimeter index for nearly all polygons falls between 0.4 and 0.6. Thus, in this step, all polygons whose perimeter index falls in this range are classified as positional errors. In the original version of the test, if the index is smaller than .25 or greater than .75, the error is categorized as attribute with the remaining polygons falling into a gray area, where it is not clear whether the error is one of position or attribute.

However, Lester and Chrisman (1991) demonstrate further the significance of the perimeter index. For polygons where the error is purely a contrived positional error, all index values fall in a narrow range around 0.5. Further, a visual inspection of the old growth overlay showed that polygons that would have fallen into the gray area were generally quite intricate in nature, frequently with internal islands. This is not a surprise considering the complexity of the two input layers. Thus, in the version of the test that I applied, polygons that would have fallen into the gray zone were instead considered to be attribute errors.

Applying the test

In an attempt to understand whether there was a consistent bias to either positional or attribute error in the two old growth datasets, I ran the Chrisman/Lester test against the two old growth coverages. This is the first time that the test has been run against two coverages with completely different provenances, against "real data" as opposed to more contrived situations. Also, the test has been applied to only relatively small areas before, such as a township. Now it is being applied at a massive scale - from central Oregon to the U.S./Canada border, over four National Forests. Furthermore, the polygons on the input layers are much more complicated than any that have been tested before. Thus, it is also a more significant "test of the test" than has been run before.

The test was run in Arc/INFO 7.1.2 on a dual Pentium workstation using AMLs adapted from the AMLs used by Lester and Chrisman. The source code for the AMLs is included as an appendix to this paper.

Because the comparison of the old growth mapping results for each of the forests shows that there were significant differences in the amount of error in each forest, we expect to see significant differences in the results of the Chrisman/Lester test across each forest. However, if there were no bias towards either kind of error, we would expect to see approximately equal proportions of each type of error in each forest.

Categories. The Wilderness Society project mapped three different categories of what they referred to as "Ancient Forest". The category they called "Old Growth" is the category of forest that meets the definition that both they and the USFS used. The other two categories included "other Ancient Forest", which met some, but not all, of the characteristics of old growth used in the definition, and "high elevation ancient forest". Because the acreage totals the Society found for ancient forest more closely match the acreage found by the USFS for old growth than the acreage the Society found for old growth, I ran the test twice. First I compared USFS old growth category against The Wilderness Society's ancient forest category, then USFS low-elevation old growth category against the more restrictive Wilderness Society's old-growth category.

Test Results

The results of the test vary widely for each forest. This is not unexpected because the overall comparison of the forests' old growth acreage varied substantially. However, it is significant that there are notable differences between the proportions of positional and attribute error. Tables 1 and 2 contain confusion matrices for the overlays. In these matrices, attribute and positional error are differentiated for the cells that are not on the main diagonal, i.e., the cells that represent disagreement, or error. Positional error in all cases represents significantly less acreage than attribute error. In most cases, across the four forests and two different overlays, and for errors of both omission and commission, positional error ranges between 1.5% and 3.5% of forest acreage.

In all cases, attribute error is at least 1.5 times higher than positional error, in most cases it is at least 2 times higher, and in one case attribute error contributes over 10 times as much error as positional error (Table 2c).

Unfortunately, because the USFS study produced what was essentially only a binary map, old growth or not old growth, these are only two-by-two confusion matrices. In the earlier example of an application of this test that involved mapping several classes, positional error is shown to be relatively symmetric across the main diagonal whereas attribute error is not at all symmetric, thus showing that the two classes of error have different distributions (Chrisman and Lester 1991). However, even in this case it can be inferred that the two classes of errors are drawn from different populations of errors and should not be conflated into the same error matrix.

Some examples of the characterization of the polygons resulting from the overlay are shown in the Figures 2 and 3. Thin polygons surrounding polygons of old growth are generally characterized as positional error. Embedded polygons are characterized as attribute error.

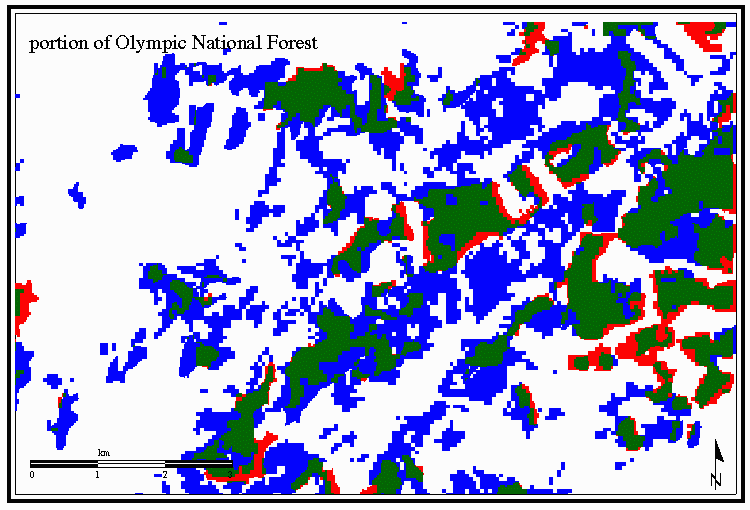
Figure 2 Example from Olympic National Forest

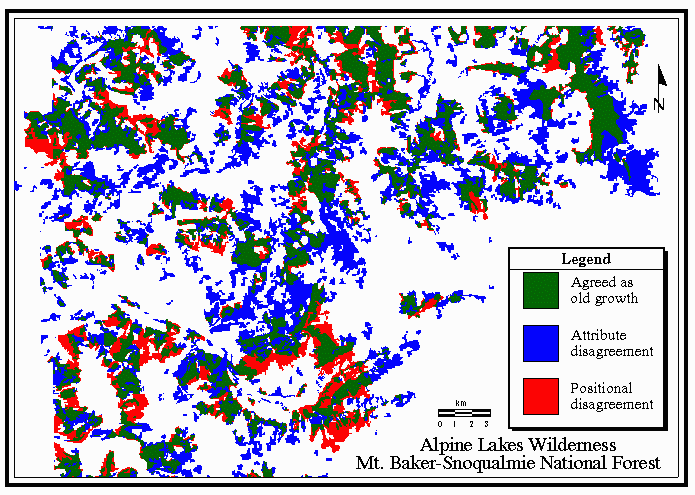
Figure 3 Example from Mt. Baker-Snoqualmie National Forest

The fact that the datasets were derived from satellite imagery is clear from characteristic stairstep edges of the polygons. The narrowness of some of the polygons identified as positional error points to the different resolution of satellite imageryused by the two projects (57m Landsat MSS for The Wilderness Society, 25m Landsat TM for the Forest Service) as a likely source for the error.

Conclusions

For the overlays of the old growth datasets, attribute error was generally a much larger component of overall error than positional error. Also, positional error was a relatively constant proportion of the error. This is consistent with the assertion that positional error generally is a result of the technology used to derive the coverage. This is confirmed by a visual check of the overlay.

A characterization of error is a necessary part of understanding the nature of a dataset and whether it is useful for a given purpose. Indeed, characterizations of attribute and positional accuracy are important components of the data quality report in the recent U.S. standards for spatial metadata (FGDC 1994). The test to distinguish positional from attribute error in overlays of categorical maps gives us one tool to make such a characterization and to yield something quantitative for a metadata report.

While the two old growth studies were later used to delineate areas to protect from logging, their more important and immediate purpose was more political - to find overall acreage figures for old growth - i.e., habitat for the endangered spotted owl. Being aware of positional error is more important when using a data set for delineating specific stands on the ground. However, attribute errors are more important when comparing overall acreages. Thus, that the more substantive disagreement between the datasets was attribute error has implications for their use in communicating old growth acreage/spotted owl territory.

Further research. This paper has used an exploratory a posteriori test to better characterize the nature of the disagreement between the two old growth datasets. Now, we can focus on identifying the sources of the two different kinds of errors. The positional error largely seems to be an artifact of the technology used. Thus, we can focus on the polygons that are categorized as purely attribute error, because these are the polygons where the two studies truly disagreed. An application of this test to a more current dataset would enable us to focus on polygons which are attribute errors, thus making a field verification more efficient.

ACKNOWLEDGEMENTS. The author wishes to thank Nick Chrisman, Dave Peterson, and anonymous reviewers for many useful suggestions for this paper.

References

Chrisman, Nicholas R. 1989. A taxonomy of cartographic error applied to categorical maps. In Proceedings, Ninth International Symposium on Computer-Assisted Cartography (Auto-Carto 9). American Society for Photogrammetry and Remote Sensing, Baltimore.

Chrisman, Nicholas R. and Marcus K. Lester. 1991. A diagnostic test for error in categorical maps. In Proceedings, Tenth International Symposium on Computer-Assisted Cartography (Auto-Carto 10). American Society for Photogrammetry and Remote Sensing, Baltimore. Pp. 330-348.

Congalton, Russell G., and Kass Green. 1993. A practical look at the sources of confusion in error matrix generation. Photogrammetric Engineering and Remote Sensing 59(5):641-644.

Congalton, Russell G., Kass Green, and John Teply. 1993. Mapping old growth forests on national forest and park lands in the Pacific Northwest from remotely sensed data. Photogrameetric Engeering and Remote Sensing 59(4):529-535.

Edwards, Geoffrey and Kim E. Lowell. 1996. Modeling uncertainty in photointerpreted boundaries. Photogrammetric Engineering and Remote Sensing 62(4): 377-391.

FGDC. 1994. Content Standards for Digital Geospatial Metadata (version 1.0). FGDC-STD-001. Federal Geographic Data Committee, Washington, D.C.

Goodchild, Michael F. and Sucharita Gopal, editors. 1989. The Accuracy of Spatial Databases. Taylor and Francis, London. 290 pages.

Goodchild, Michael F., Sun Guoqing, and Yang Shiren. 1992. Development and test of an error model for categorical data. International Journal of Geographical Information Systems 6(2): 87-104.

Hirt, Paul W. 1994. A Conspiracy of Optimism: Management of the National Forests since World War Two. University of Nebraska Press, Lincoln. 416 pages.

Lester, Marcus K. and Chrisman, Nicholas R., 1991. Not all slivers are skinny: A comparison of two methods for detecting positional errors in categorical maps. In Proceedings, GIS/ LIS '91. American Society for Photogrammetry and Remote Sensing, Baltimore. Vol. 2, 648-658.

Lowell, Kim E. 1994. An uncertainty-based spatial representation for natural resources phenomena. In Advances in GIS Research: Proceedings of the Sixth International Symposium on Spatial Data Handling. London, Taylor and Francis. Vol. 2, 933-944.

Lowell, Kim E. and Geoffrey Edwards 1996. Modeling heterogeneity and change in natural forests. Geomatica 50(4): 425-440.

Morrison, Peter H., Deanne Kloepfer, David A. Leversee, Caroline M. Socha, Deborah L. Ferber. 1991. Ancient Forests in the Pacific Northwest: Analysis and Maps of Twelve National Forests. The Wilderness Society, Washington, D.C. 24 pages.

Norheim, Robert A. 1996. Is there an Answer to Mapping Old Growth? An Examination of Two Projects Conducted with Remote Sensing and GIS. Unpublished Masters thesis. Department of Geography, University of Washington, Seattle. 150 pages.

Norheim, Robert A. 1997. Dueling databases: examining the differences between two old growth mapping projects. Paper given at Thirteenth International Symposium on Computer-assisted Cartography (Auto-Carto 13), at Seattle. Available on the web at the URL http://purl.oclc.org/net/norheim/oldgrowth/dueling-db.html

Unwin, David J. 1981. Introductory Spatial Analysis. Methuen, London. 212 pages.

Yaffee, Steven L. 1994. The Wisdom of the Spotted Owl: Policy Lessons for a New Century. Island Press, Washington, D.C. 430 pages.

Last updated: July 20, 1998

Copyright 1996-98 Robert A. Norheim and IGU GISc Study Group