Finite state machine

Excerpts from Chapter 6 in The Way of Z. Sections explaining the motivation are omitted here.

This page looks best when this and this X are about the same size: X. See these viewing tips.

Here we show three ways to represent a finite state machine model: a diagram, a table, and Z.

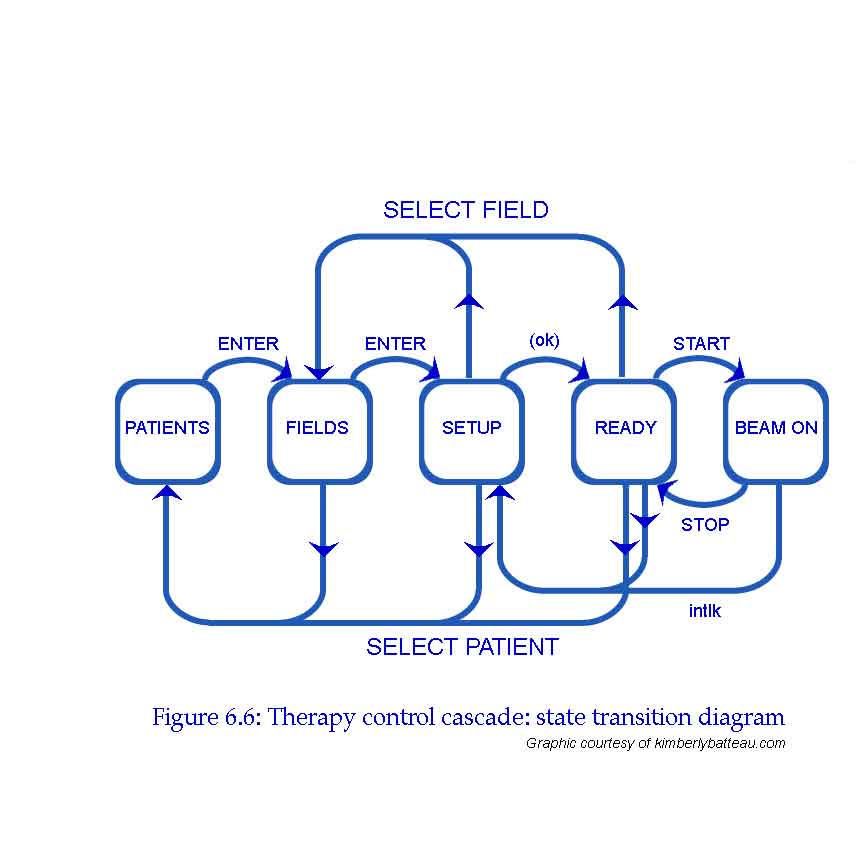
States are indicated by bubbles; transitions between states by arrows. The arrows are labelled with the events that cause state transitions. Thus, in the PATIENTS state pressing the ENTER key causes a transition to the FIELDS state, but in the FIELDS state pressing ENTER gets you to SETUP.

We can trace all possible treatment sequences by following the arrows around the diagram.

State transition table

The state transition diagram is a picture of our state machine model. There are other ways to represent the same model. Here is the state transition table.

Entries in the table indicate the next state that is reached when the event indicated by the column heading occurs during the state indicated by the row heading.

This table is a bit more explicit than the state transition diagram because it makes it clear when events are ignored. For example, pressing the SELECT PATIENT key in the BEAM ON mode has no effect (causes no state change); this is indicated by the hyphen --- in the table. Including all of these in the diagram would make it too cluttered. As notations grow more formal, they become more explicit and rely less on unwritten assumptions.

Z notation

Finally, we express the state machine model in Z. Don't worry about the details of the notation for now. You should be able to see that the function transitions models the state transition table. For example, the expression (patients,enter) fields corresponds to the single transition in the first row of the table: when the patients screen is displayed, pressing enter displays the fields screen. Likewise, (fields, select_patient) patients,(fields, enter) setup represents the two transitions in the second row of the table.

STATE ::= patients | fields | setup | ready | beam_on

FSM == (STATE $\cross$ EVENT) $\pfun$ STATE

$\begin{axdef}$
		no_change, transitions, control: FSM

	$\where$

		control = no_change $\oplus$ transitions

		no_change = { s: STATE; e: EVENT (s, e) $\mapsto$ s }

		transitions = { (patients, enter) $\mapsto$ fields,

		(fields, select_patient) $\mapsto$ patients, (fields, enter) $\mapsto$ setup,

		(setup, select_patient) $\mapsto$ patients, (setup, select_field) $\mapsto$ fields, (setup, ok) $\mapsto$ ready,

		(ready, select_patient) $\mapsto$ patients, (ready, select_field) $\mapsto$ fields, (ready, start) $\mapsto$ beam_on, (ready, intlk) $\mapsto$ setup,

		(beam_on, stop) $\mapsto$ ready, (beam_on, intlk) $\mapsto$ setup }
	$\end{axdef}$

This is the most explicit version yet. The definition of no_change spells out what was left to convention before: in certain states, certain inputs do not cause a state change.

This example already illustrates two of the most powerful concepts in formal methods: using compact symbolic expressions to represent lots of cases in a little space, and using operators to build up complex formulas from simpler ones.

State transition tables are often very sparse: most of the entries are empty "nothing changes" cells that make the tables large and difficult to read. In Z we don't have to enumerate all the no_change transitions as we did in the table --- we can do it symbolically; no_change is actually a state machine that does nothing. We define a second machine, transitions, that includes only the transitions where something actually happens. Then we use the Z override operator to combine the two. The expression no_change transitions describes the state machine that behaves as no_change, except when there is a relevant entry in transitions.

More importantly, the diagram and the table are specialized notations that only work for finite state machines. We cannot use them to attack the hard parts of the problem that I left out of this toy example. For example, what really distinguishes the state READY from SETUP? We glossed over this --- we merely said the system becomes ready when the ok event occurs. This mysterious ok event does not come from a key or button; we left it undefined. But we must define it; this transition is the central safety-critical event in the program because it closes the relay that allows the beam to turn on.

In READY, all the settings match their prescribed values; the ok event occurs when the system achieves this condition. (In fact, some settings must match exactly, while others are permitted to vary within a tolerance; some settings that don't match can be overridden, while others cannot. And so on.) We cannot represent this with our diagrams or tables because it involves dozens of settings that vary over continuous ranges. We need to model values and relations between values. We will see how when we develop a more complete model of this program in chapters 21 and 22.

Finite State Machine

State transition diagram

State transition table

Z notation

	SELECT PATIENT	SELECT FIELD	ENTER	ok	START	STOP	intlk
PATIENTS	---	---	FIELDS	---	---	---	---
FIELDS	PATIENTS	---	SETUP	---	---	---	---
SETUP	PATIENTS	FIELDS	---	READY	---	---	---
READY	PATIENTS	FIELDS	---	---	BEAM ON	---	SETUP
BEAM ON	---	---	---	---	---	READY	SETUP