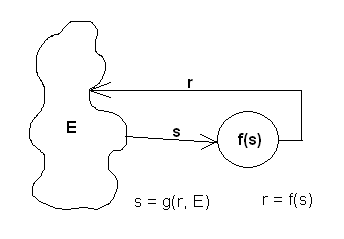

The stimulus-response model is based on the concept of homeostasis - the tendancy for a biological system to maintain a stable internal milieu. Environmental stimuli destablize the internal conditions (e.g., pH, temperature, chemical constituents, etc.). A biological system maintains chemical mechanisms that act to counteract these destablizing conditions.
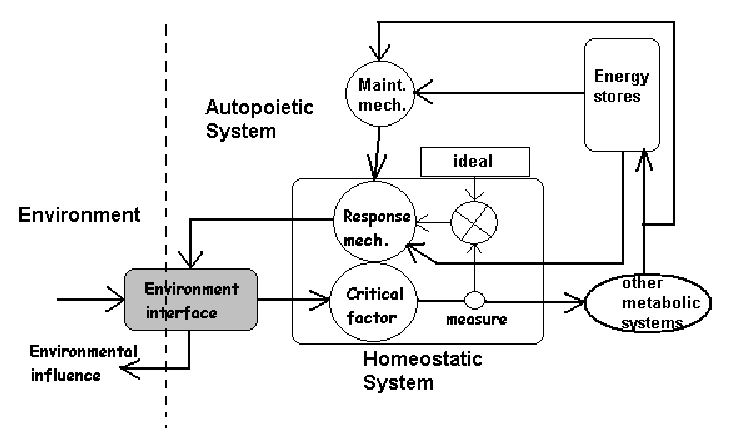
If a system does not respond to the stimulus, damage will accrue internally. The biological work that is needed to repair such damage has an associated energy cost. So the point of response is to minimize this damage and its cost [NOTE: if damage is too high the organism dies!]
Additional costs accrue. There is a cost associated with the actual work of responding itself. We can assume, however, that the cost of responding is significantly less than the cost associated with repairing damage (otherwise what would be the point!) There is also a cost associated with the on-going maintenance of the physiological subsystems needed to do the responding. Complex biological molecules have a madening tendancy to degrade at physiological temperatures. Thus work must be continually done to maintain the system. Again we may assume that this cost is substantially less than either the cost of responding or the cost of repairing damage.
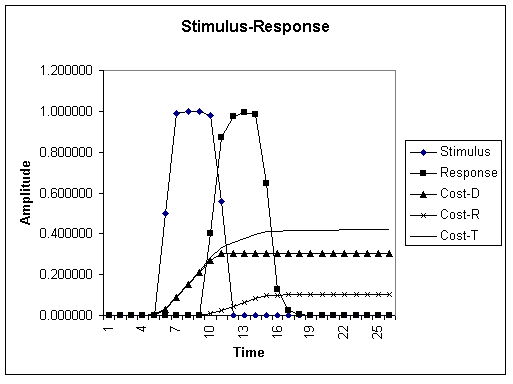
The graph shows a stimulus-response model with accumulating costs of repairing damage (Cost-D) and responding (Cost-R) as well as total cost (Cost-T). Not shown is the cost of maintenance which is negligable relative to the two (more dynamic and dramatic) costs due to the effects of a stimulus. Note that since there is a time lag between the onset of the stimulus and the peak response, the cost of damage increases until the cost of responding starts rising. All costs can be accounted for by energy deficits. The organism needs to replenish its energy (and material) stores in order to off-set these costs.