CSS437 Introduction to Robotics
Control Theory
Cybernetics - the science of control in systems. Norbert Weiner.
Stability
A controlled process maintains output values within critical limits
External influences disturb the stability of the process
Open-loop control
When no outside influences can disturb the functioning of a process.
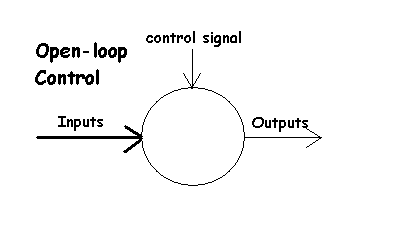Not very likely in the real world of mobile, autonomous robots!!!
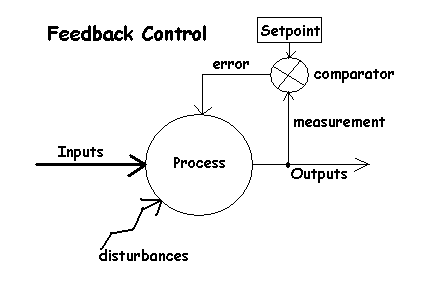
Principle of feedback - Closed-loop control in the "real" world
Feedback works by counteracting the effects of a disturbance or error in
desired vs. actual.
Measuring a critical output parameter
Comparing it to an ideal value (setpoint)
Using error to adjust the process
Error has both direction and magnatude
Proportional Control
In proportional control, the control signal, C, is proportional to the
direction and magnatude of the error signal.
C = k0 e
where k0 is a gain constant (note that it is posible
to introduce more complex functions including non-linear ones but this
is problematic in most cases).
Problems
Overcompensation and oscillations. Inertia. Non-linearity.
Derivative Control
In derivative control, the control signal is proportional to the rate of
change in the error signal (not a pure control strategy). Used to adjust
the overall gain and damp oscillations.
C = k1 de/dt
Integrative Control
In integrative control, the control signal is proportional to the integral
of error over some time frame. Ususally implelented as a moving average.
(Also not a pure control strategy). Used to smooth the response of
a control signal.
C = k2 I e(t)
dt
PID Control
Combining these three sources of information into a single control signal
provides the greatest stability in systems with high degrees of disturbance
and control inertia.
C = k0 e + k1
de/dt + k2 I e(t)
dt
The relative influences of error, rate of change in error and average
error over time are controlled by the gain constants, k0,
k1 and k2. Combinational controls
such as PD or PI are possible.
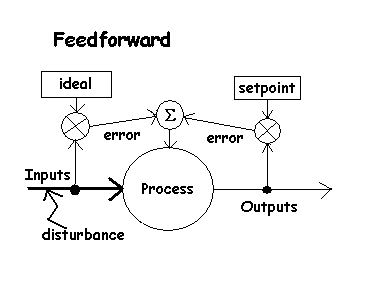
Feedforward Control - Anticipation
The purpose of feedforward control is to take preemptive action in order
to further reduce the effects of oscillation or lag in adjusting the control.
It assumes that a disturbance will change the values of inputs from the
ideal. Adjustments to the control signal can be made before a noticable
effect is measured at the output.
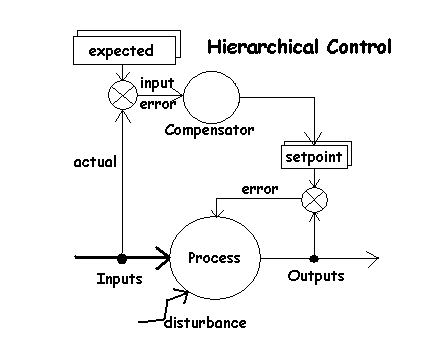
Hierarchical Control
A more sophisticated form of control. This form assumes that there
are multiple inputs and outputs which can be varied to produce an optimal
mix of desired outputs.
Adaptive Control
The most sophisticated controllers combine hierarchical and feedforward
mechanisms in multiple layers. Adaptive controllers include memory
and models of the environment to further refine anticipatory action.
Models of the environment are modifiable over time to compensate for changes
in the environment.